| Introduction |
| Background: |
| Particles |
| QCD |
| Bosons |
| Uncertainty |
| Principal: |
| Interaction |
| Parton |
| Variables |
| Jets |
| Psedorap. |
| Next |
| Previous |
Jets
In photon-proton scattering, one of the quarks in the photon interacts with one of the quarks of the proton. That causes the disintegration of the proton as it is no longer allowed to exist as it is no longer colour neutral and one of the basic rules of particles physics states that all hadrons must be colour neutral as they do not feel the strong force. The quarks left from this disintegration and undergo the hadronisation process thus creating showers of hadronic particles arranged in jets.
In the centre of mass system (CMS), those jets are diametrically opposed and, apart from the azimuthal angle f, a single polar angle q* is sufficient to describe the jets distribution. q* is then defined as being the angle between the jet direction and the beam axis. However, due to the particles very high momentum, this picture of the jets is Lorrentz transformed in the laboratory frame of reference. The difference between the two frames is clearly shown in figures 1 and 2 below.
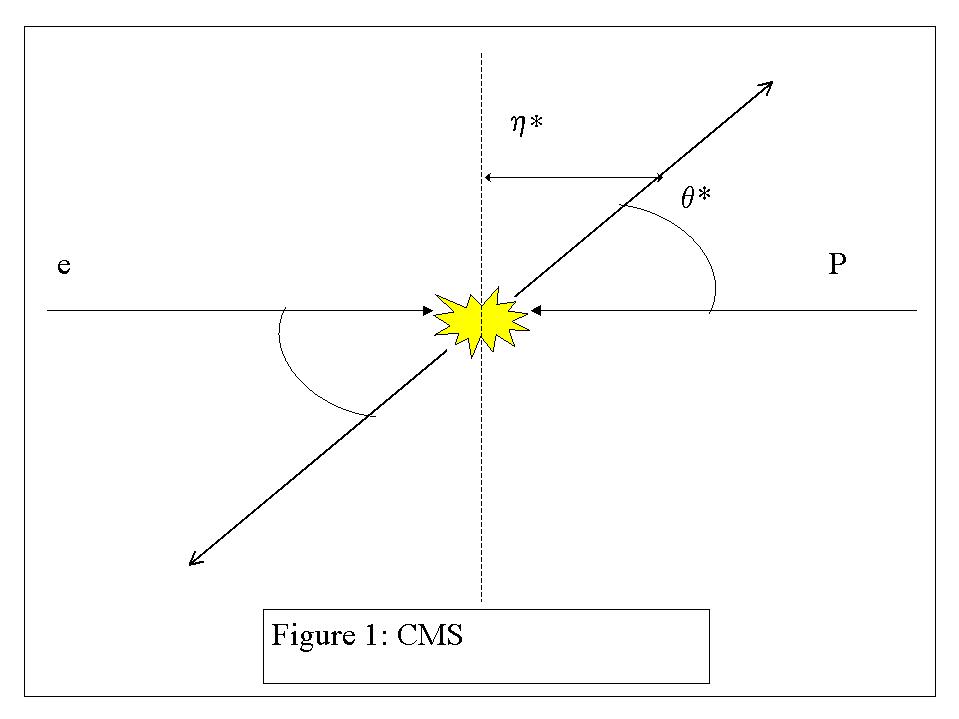
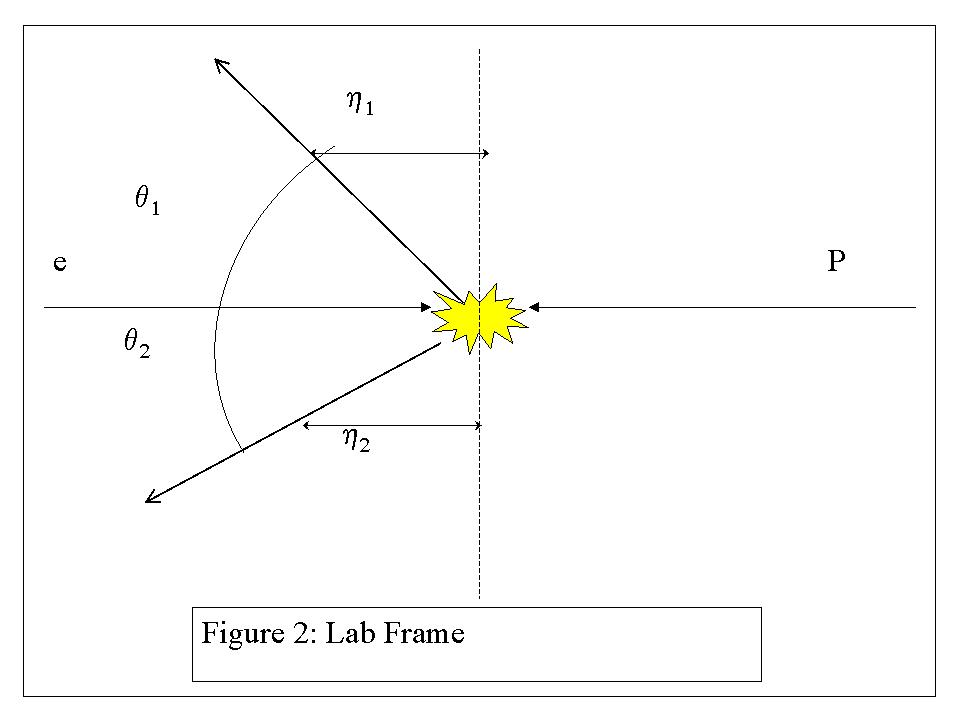
Now, we have seen that we could use the pseudorapidity to represent the angle q of the laboratory in the CMS. From there, we find that the pseudoraptidity in the particles' frame of reference is equal to:
h* = - ln tan ( q* / 2 )
and in the lab frame of reference, as the rapidities are shifted by a constant factor B from the CMS ones, we find that the pseudorapidities then satisfy the following equations:
h1 = B - h*
and h2 = B + h*
Solving the above two equations for h* and B using linear combination, where h* represents the scattering angle in the CMS, and B the constant shift in the rapidity:
h* = (1/2) | h1 - h2 |
and B = (1/2) (h1 + h2)
From those two equations, we can see that the boost is simply the average pseudorapidity of the two jets, and the CMS jet rapidity is half the difference between them.
The boost is an indication of how much momentum the incoming partons carry from the photon and the proton. The momentum fractions xp and xg carried by the incoming partons will determine the boost: if we assume that both jets have equal transverse energy, we can show that
B = (1/2) ln [(xpOBS Ep)/(xgOBS yEe)]
Hence, if we consider the boost B we can study the inner structures of the proton and the photon. This is the aim of this project.