Summation to Calculate Two-Particle Joint W SDM Elements

In this appendix the summations of operators needed to calculate all 81 elements of the two-particle joint Spin Density Matrix are listed. In each equation $\theta_{f_{1}}$ is the polar angle and $\phi_{f_{1}}$ is the azimuthal angle of the decay fermion from the ${\rm W}^{-}$ in the ${\rm W}^{-}$ rest frame. $\theta_{\bar{f}_{4}}$ is the polar angle and $\phi_{\bar{f}_{1}}$ is the azimuthal angle of the decay anti-fermion from the ${\rm W}^{+}$ in the ${\rm W}^{+}$ rest frame. The elements are extracted in bins of $\cos\theta_{\rm W}$, the ${\rm W}^{-}$ production angle. $k$ is the bin of $\cos\theta_{\rm W}$ and $N_{k}$ is the number of events in that bin.

$$Re\left(\rho_{++++}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{1}{4}(5\cos^{2}\theta_{f_{... ...eta_{f_{1}} - 1)(5\cos^{2}\theta_{\bar{f}_{4}} + 2\cos\theta_{\bar{f}_{4}} - 1)$$

$$Im\left(\rho_{++++}(k)\right) =$$ 0

$$Re\left(\rho_{+++0}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{-4}{3\pi\sqrt{2}}(5\cos^{2... ...} - 2\cos\theta_{f_{1}} - 1)(1+4\cos\theta_{\bar{f}_{4}})\cos\phi_{\bar{f}_{4}}$$

$$Im\left(\rho_{+++0}(k)\right) = -\frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{4}{3\pi\sqrt{2}}(5\cos^{2... ...} - 2\cos\theta_{f_{1}} - 1)(1+4\cos\theta_{\bar{f}_{4}})\sin\phi_{\bar{f}_{4}}$$

$$Re\left(\rho_{+++-}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}(5\cos^{2}\theta_{f_{1}} - 2\cos\theta_{f_{1}} - 1)\cos2\phi_{\bar{f}_{4}}$$

$$Im\left(\rho_{+++-}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}-(5\cos^{2}\theta_{f_{1}} - 2\cos\theta_{f_{1}} - 1)\sin2\phi_{\bar{f}_{4}}$$

$$Re\left(\rho_{++0+}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{4}{3\pi\sqrt{2}}(5\cos^{2}... ...} - 2\cos\theta_{f_{1}} - 1)(1+4\cos\theta_{\bar{f}_{4}})\cos\phi_{\bar{f}_{4}}$$

$$Im\left(\rho_{++0+}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{4}{3\pi\sqrt{2}}(5\cos^{2}... ...} - 2\cos\theta_{f_{1}} - 1)(1+4\cos\theta_{\bar{f}_{4}})\sin\phi_{\bar{f}_{4}}$$

$$Re\left(\rho_{++00}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{1}{2}(5\cos^{2}\theta_{f_{1}} - 2\cos\theta_{f_{1}} - 1)(2-5\cos^{2}\theta_{\bar{f}_{4}})$$

$$Im\left(\rho_{++00}(k)\right) =$$ 0

$$Re\left(\rho_{++0-}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{4}{3\pi\sqrt{2}}(5\cos^{2}... ...} - 2\cos\theta_{f_{1}} - 1)(1-4\cos\theta_{\bar{f}_{4}})\cos\phi_{\bar{f}_{4}}$$

$$Im\left(\rho_{++0-}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{-4}{3\pi\sqrt{2}}(5\cos^{2... ...} - 2\cos\theta_{f_{1}} - 1)(1-4\cos\theta_{\bar{f}_{4}})\sin\phi_{\bar{f}_{4}}$$

$$Re\left(\rho_{++-+}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}(5\cos^{2}\theta_{f_{1}} - 2\cos\theta_{f_{1}} - 1)\cos2\phi_{\bar{f}_{4}}$$

$$Im\left(\rho_{++-+}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}(5\cos^{2}\theta_{f_{1}} - 2\cos\theta_{f_{1}} - 1)\sin2\phi_{\bar{f}_{4}}$$

$$Re\left(\rho_{++-0}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{4}{3\pi\sqrt{2}}(5\cos^{2}... ...} - 2\cos\theta_{f_{1}} - 1)(1-4\cos\theta_{\bar{f}_{4}})\cos\phi_{\bar{f}_{4}}$$

$$Im\left(\rho_{++-0}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{4}{3\pi\sqrt{2}}(5\cos^{2}... ...} - 2\cos\theta_{f_{1}} - 1)(1-4\cos\theta_{\bar{f}_{4}})\sin\phi_{\bar{f}_{4}}$$

$$Re\left(\rho_{++--}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{1}{4}(5\cos^{2}\theta_{f_{... ...eta_{f_{1}} - 1)(5\cos^{2}\theta_{\bar{f}_{4}} - 2\cos\theta_{\bar{f}_{4}} - 1)$$

$$Im\left(\rho_{++--}(k)\right) =$$ 0

$$Re\left(\rho_{+0++}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{-4}{3\pi\sqrt{2}}(1-4\cos\... ...\cos\phi_{f_{1}}(5\cos^{2}\theta_{\bar{f}_{4}} + 2\cos\theta_{\bar{f}_{4}} - 1)$$

$$Im\left(\rho_{+0++}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{4}{3\pi\sqrt{2}}(1-4\cos\t... ...\sin\phi_{f_{1}}(5\cos^{2}\theta_{\bar{f}_{4}} + 2\cos\theta_{\bar{f}_{4}} - 1)$$

$$Re\left(\rho_{+0+0}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{-32}{9\pi^{2}}((1-4\cos\theta_{f_{1}})\cos\phi_{f_{1}}(1+4\cos\theta_{\bar{f}_{4}})\cos\phi_{\bar{f}_{4}}$$

$$- (1-4\cos\theta_{f_{1}})\sin\phi_{f_{1}}(1+4\cos\theta_{\bar{f}_{4}})\sin\phi_{\bar{f}_{4}})$$

$$Im\left(\rho_{+0+0}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{32}{9\pi^{2}}((1-4\cos\theta_{f_{1}})\cos\phi_{f_{1}}(1+4\cos\theta_{\bar{f}_{4}})\sin\phi_{\bar{f}_{4}}$$

$$+ (1-4\cos\theta_{f_{1}})\sin\phi_{f_{1}}(1+4\cos\theta_{\bar{f}_{4}})\cos\phi_{\bar{f}_{4}})$$

$$Re\left(\rho_{+0+-}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{-8\sqrt{2}}{3\pi}((1-4\cos\theta_{f_{1}})\cos\phi_{f_{1}}\cos2\phi_{\bar{f}_{4}}$$

$$- (1-4\cos\theta_{f_{1}})\sin\phi_{f_{1}}\sin2\phi_{\bar{f}_{4}})$$

$$Im\left(\rho_{+0+-}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{8\sqrt{2}}{3\pi}((1-4\cos\theta_{f_{1}})\cos\phi_{f_{1}}\sin2\phi_{\bar{f}_{4}}$$

$$+ (1-4\cos\theta_{f_{1}})\sin\phi_{f_{1}}\cos2\phi_{\bar{f}_{4}})$$

$$Re\left(\rho_{+00+}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{-32}{9\pi^{2}}((1-4\cos\theta_{f_{1}})\cos\phi_{f_{1}}(1+4\cos\theta_{\bar{f}_{4}})\cos\phi_{\bar{f}_{4}}$$

$$+ (1-4\cos\theta_{f_{1}})\sin\phi_{f_{1}}(1+4\cos\theta_{\bar{f}_{4}})\sin\phi_{\bar{f}_{4}})$$

$$Im\left(\rho_{+00+}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{-32}{9\pi^{2}}((1-4\cos\theta_{f_{1}})\cos\phi_{f_{1}}(1+4\cos\theta_{\bar{f}_{4}})\sin\phi_{\bar{f}_{4}}$$

$$- (1-4\cos\theta_{f_{1}})\sin\phi_{f_{1}}(1+4\cos\theta_{\bar{f}_{4}})\cos\phi_{\bar{f}_{4}})$$

$$Re\left(\rho_{+000}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{-8}{3\pi\sqrt{2}}(1-4\cos\theta_{f_{1}})\cos\phi_{f_{1}}(2-5\cos^{2}\theta_{\bar{f}_{4}})$$

$$Im\left(\rho_{+000}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{8}{3\pi\sqrt{2}}(1-4\cos\theta_{f_{1}})\sin\phi_{f_{1}}(2-5\cos^{2}\theta_{\bar{f}_{4}})$$

$$Re\left(\rho_{+00-}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{-32}{9\pi^{2}}((1-4\cos\theta_{f_{1}})\cos\phi_{f_{1}}(1-4\cos\theta_{\bar{f}_{4}})\cos\phi_{\bar{f}_{4}}$$

$$- (1-4\cos\theta_{f_{1}})\sin\phi_{f_{1}}(1-4\cos\theta_{\bar{f}_{4}})\sin\phi_{\bar{f}_{4}})$$

$$Im\left(\rho_{+00-}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{32}{9\pi^{2}}((1-4\cos\theta_{f_{1}})\cos\phi_{f_{1}}(1-4\cos\theta_{\bar{f}_{4}})\sin\phi_{\bar{f}_{4}}$$

$$+ (1-4\cos\theta_{f_{1}})\sin\phi_{f_{1}}(1-4\cos\theta_{\bar{f}_{4}})\cos\phi_{\bar{f}_{4}})$$

$$Re\left(\rho_{+0-+}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{-8\sqrt{2}}{3\pi}((1-4\cos\theta_{f_{1}})\cos\phi_{f_{1}}\cos2\phi_{\bar{f}_{4}}$$

$$+ (1-4\cos\theta_{f_{1}})\sin\phi_{f_{1}}\sin2\phi_{\bar{f}_{4}})$$

$$Im\left(\rho_{+0-+}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{-8\sqrt{2}}{3\pi}((1-4\cos\theta_{f_{1}})\cos\phi_{f_{1}}\sin2\phi_{\bar{f}_{4}}$$

$$- (1-4\cos\theta_{f_{1}})\sin\phi_{f_{1}}\cos2\phi_{\bar{f}_{4}})$$

$$Re\left(\rho_{+0-0}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{-32}{9\pi^{2}}((1-4\cos\theta_{f_{1}})\cos\phi_{f_{1}}(1-4\cos\theta_{\bar{f}_{4}})\cos\phi_{\bar{f}_{4}}$$

$$+ (1-4\cos\theta_{f_{1}})\sin\phi_{f_{1}}(1-4\cos\theta_{\bar{f}_{4}})\sin\phi_{\bar{f}_{4}})$$

$$Im\left(\rho_{+0-0}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{-32}{9\pi^{2}}((1-4\cos\theta_{f_{1}})\cos\phi_{f_{1}}(1-4\cos\theta_{\bar{f}_{4}})\sin\phi_{\bar{f}_{4}}$$

$$- (1-4\cos\theta_{f_{1}})\sin\phi_{f_{1}}(1-4\cos\theta_{\bar{f}_{4}})\cos\phi_{\bar{f}_{4}})$$

$$Re\left(\rho_{+0--}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{-4}{3\pi\sqrt{2}}(1-4\cos\... ...\cos\phi_{f_{1}}(5\cos^{2}\theta_{\bar{f}_{4}} - 2\cos\theta_{\bar{f}_{4}} - 1)$$

$$Im\left(\rho_{+0--}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{4}{3\pi\sqrt{2}}(1-4\cos\t... ...\sin\phi_{f_{1}}(5\cos^{2}\theta_{\bar{f}_{4}} - 2\cos\theta_{\bar{f}_{4}} - 1)$$

$$Re\left(\rho_{+-++}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\cos2\phi_{f_{1}}(5\cos^{2}\theta_{\bar{f}_{4}} + 2\cos\theta_{\bar{f}_{4}} - 1)$$

$$Im\left(\rho_{+-++}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}-\sin2\phi_{f_{1}}(5\cos^{2}\theta_{\bar{f}_{4}} + 2\cos\theta_{\bar{f}_{4}} - 1)$$

$$Re\left(\rho_{+-+0}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{8\sqrt{2}}{3\pi}(\cos2\phi_{f_{1}}(1+4\cos\theta_{\bar{f}_{4}})\cos\phi_{\bar{f}_{4}}$$

$$- \sin2\phi_{f_{1}}(1+4\cos\theta_{\bar{f}_{4}})\sin\phi_{\bar{f}_{4}})$$

$$Im\left(\rho_{+-+0}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{-8\sqrt{2}}{3\pi}(\cos2\phi_{f_{1}}(1+4\cos\theta_{\bar{f}_{4}})\sin\phi_{\bar{f}_{4}}$$

$$+ \sin2\phi_{f_{1}}(1+4\cos\theta_{\bar{f}_{4}})\cos\phi_{\bar{f}_{4}})$$

$$Re\left(\rho_{+-+-}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}4(\cos2\phi_{f_{1}}\cos2\phi_{\bar{f}_{4}}- \sin2\phi_{f_{1}}\sin2\phi_{\bar{f}_{4}})$$

$$Im\left(\rho_{+-+-}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}-4(\cos2\phi_{f_{1}}\sin2\phi_{\bar{f}_{4}}+\sin2\phi_{f_{1}}\cos2\phi_{\bar{f}_{4}})$$

$$Re\left(\rho_{+-0+}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{8\sqrt{2}}{3\pi}(\cos2\phi_{f_{1}}(1+4\cos\theta_{\bar{f}_{4}})\cos\phi_{\bar{f}_{4}}$$

$$+ \sin2\phi_{f_{1}}(1+4\cos\theta_{\bar{f}_{4}})\sin\phi_{\bar{f}_{4}})$$

$$Im\left(\rho_{+-0+}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{8\sqrt{2}}{3\pi}(\cos2\phi_{f_{1}}(1+4\cos\theta_{\bar{f}_{4}})\sin\phi_{\bar{f}_{4}}$$

$$- \sin2\phi_{f_{1}}(1+4\cos\theta_{\bar{f}_{4}})\cos\phi_{\bar{f}_{4}})$$

$$Re\left(\rho_{+-00}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}2\cos2\phi_{f_{1}}(2-5\cos^{2}\theta_{\bar{f}_{4}})$$

$$Im\left(\rho_{+-00}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}-2\sin2\phi_{f_{1}}(2-5\cos^{2}\theta_{\bar{f}_{4}})$$

$$Re\left(\rho_{+-0-}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{8\sqrt{2}}{3\pi}(\cos2\phi_{f_{1}}(1-4\cos\theta_{\bar{f}_{4}})\cos\phi_{\bar{f}_{4}}$$

$$- \sin2\phi_{f_{1}}(1-4\cos\theta_{\bar{f}_{4}})\sin\phi_{\bar{f}_{4}})$$

$$Im\left(\rho_{+-0-}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{-8\sqrt{2}}{3\pi}(\cos2\phi_{f_{1}}(1-4\cos\theta_{\bar{f}_{4}})\sin\phi_{\bar{f}_{4}}$$

$$+ \sin2\phi_{f_{1}}(1-4\cos\theta_{\bar{f}_{4}})\cos\phi_{\bar{f}_{4}})$$

$$Re\left(\rho_{+--+}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}4(\cos2\phi_{f_{1}}\cos2\phi_{\bar{f}_{4}}+\sin2\phi_{f_{1}}\sin2\phi_{\bar{f}_{4}})$$

$$Im\left(\rho_{+--+}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}4(\cos2\phi_{f_{1}}\sin2\phi_{\bar{f}_{4}}-\sin2\phi_{f_{1}}\cos2\phi_{\bar{f}_{4}})$$

$$Re\left(\rho_{+--0}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{8\sqrt{2}}{3\pi}(\cos2\phi_{f_{1}}(1-4\cos\theta_{\bar{f}_{4}})\cos\phi_{\bar{f}_{4}}$$

$$+ \sin2\phi_{f_{1}}(1-4\cos\theta_{\bar{f}_{4}})\sin\phi_{\bar{f}_{4}})$$

$$Im\left(\rho_{+--0}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{8\sqrt{2}}{3\pi}(\cos2\phi_{f_{1}}(1-4\cos\theta_{\bar{f}_{4}})\sin\phi_{\bar{f}_{4}}$$

$$- \sin2\phi_{f_{1}}(1-4\cos\theta_{\bar{f}_{4}})\cos\phi_{\bar{f}_{4}})$$

$$Re\left(\rho_{+---}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\cos2\phi_{f_{1}}(5\cos^{2}\theta_{\bar{f}_{4}} - 2\cos\theta_{\bar{f}_{4}} - 1)$$

$$Im\left(\rho_{+---}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}-\sin2\phi_{f_{1}}(5\cos^{2}\theta_{\bar{f}_{4}} - 2\cos\theta_{\bar{f}_{4}} - 1)$$

$$Re\left(\rho_{0+++}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{-4}{3\pi\sqrt{2}}(1-4\cos\... ...\cos\phi_{f_{1}}(5\cos^{2}\theta_{\bar{f}_{4}} + 2\cos\theta_{\bar{f}_{4}} - 1)$$

$$Im\left(\rho_{0+++}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{-4}{3\pi\sqrt{2}}(1-4\cos\... ...\cos\phi_{f_{1}}(5\cos^{2}\theta_{\bar{f}_{4}} + 2\cos\theta_{\bar{f}_{4}} - 1)$$

$$Re\left(\rho_{0++0}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{-32}{9\pi^{2}}((1-4\cos\theta_{f_{1}})\cos\phi_{f_{1}}(1+4\cos\theta_{\bar{f}_{4}})\cos\phi_{\bar{f}_{4}}$$

$$+ (1-4\cos\theta_{f_{1}})\sin\phi_{f_{1}}(1+4\cos\theta_{\bar{f}_{4}})\sin\phi_{\bar{f}_{4}})$$

$$Im\left(\rho_{0++0}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{32}{9\pi^{2}}((1-4\cos\theta_{f_{1}})\cos\phi_{f_{1}}(1+4\cos\theta_{\bar{f}_{4}})\sin\phi_{\bar{f}_{4}}$$

$$- (1-4\cos\theta_{f_{1}})\sin\phi_{f_{1}}(1+4\cos\theta_{\bar{f}_{4}})\cos\phi_{\bar{f}_{4}})$$

$$Re\left(\rho_{0++-}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{-8\sqrt{2}}{3\pi}((1-4\cos\theta_{f_{1}})\cos\phi_{f_{1}}\cos2\phi_{\bar{f}_{4}}$$

$$+ (1-4\cos\theta_{f_{1}})\sin\phi_{f_{1}}\sin2\phi_{\bar{f}_{4}})$$

$$Im\left(\rho_{0++-}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{8\sqrt{2}}{3\pi}((1-4\cos\theta_{f_{1}})\cos\phi_{f_{1}}\sin2\phi_{\bar{f}_{4}}$$

$$- (1-4\cos\theta_{f_{1}})\sin\phi_{f_{1}}\cos2\phi_{\bar{f}_{4}})$$

$$Re\left(\rho_{0+0+}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{-32}{9\pi^{2}}((1-4\cos\theta_{f_{1}})\cos\phi_{f_{1}}(1+4\cos\theta_{\bar{f}_{4}})\cos\phi_{\bar{f}_{4}}$$

$$- (1-4\cos\theta_{f_{1}})\sin\phi_{f_{1}}(1+4\cos\theta_{\bar{f}_{4}})\sin\phi_{\bar{f}_{4}})$$

$$Im\left(\rho_{0+0+}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{-32}{9\pi^{2}}((1-4\cos\theta_{f_{1}})\cos\phi_{f_{1}}(1+4\cos\theta_{\bar{f}_{4}})\sin\phi_{\bar{f}_{4}}$$

$$+ (1-4\cos\theta_{f_{1}})\sin\phi_{f_{1}}(1+4\cos\theta_{\bar{f}_{4}})\cos\phi_{\bar{f}_{4}})$$

$$Re\left(\rho_{0+00}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{-8}{3\pi\sqrt{2}}(1-4\cos\theta_{f_{1}})\cos\phi_{f_{1}}(2-5\cos^{2}\theta_{\bar{f}_{4}})$$

$$Im\left(\rho_{0+00}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{-8}{3\pi\sqrt{2}}(1-4\cos\theta_{f_{1}})\sin\phi_{f_{1}}(2-5\cos^{2}\theta_{\bar{f}_{4}})$$

$$Re\left(\rho_{0+0-}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{-32}{9\pi^{2}}((1-4\cos\theta_{f_{1}})\cos\phi_{f_{1}}(1-4\cos\theta_{\bar{f}_{4}})\cos\phi_{\bar{f}_{4}}$$

$$+ (1-4\cos\theta_{f_{1}})\sin\phi_{f_{1}}(1-4\cos\theta_{\bar{f}_{4}})\sin\phi_{\bar{f}_{4}})$$

$$Im\left(\rho_{0+0-}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{32}{9\pi^{2}}((1-4\cos\theta_{f_{1}})\cos\phi_{f_{1}}(1-4\cos\theta_{\bar{f}_{4}})\sin\phi_{\bar{f}_{4}}$$

$$- (1-4\cos\theta_{f_{1}})\sin\phi_{f_{1}}(1-4\cos\theta_{\bar{f}_{4}})\cos\phi_{\bar{f}_{4}})$$

$$Re\left(\rho_{0+-+}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{-8\sqrt{2}}{3\pi}((1-4\cos\theta_{f_{1}})\cos\phi_{f_{1}}\cos2\phi_{\bar{f}_{4}}$$

$$- (1-4\cos\theta_{f_{1}})\sin\phi_{f_{1}}\sin2\phi_{\bar{f}_{4}})$$

$$Im\left(\rho_{0+-+}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{-8\sqrt{2}}{3\pi}((1-4\cos\theta_{f_{1}})\cos\phi_{f_{1}}\sin2\phi_{\bar{f}_{4}}$$

$$+ (1-4\cos\theta_{f_{1}})\sin\phi_{f_{1}}\cos2\phi_{\bar{f}_{4}})$$

$$Re\left(\rho_{0+-0}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{-32}{9\pi^{2}}((1-4\cos\theta_{f_{1}})\cos\phi_{f_{1}}(1-4\cos\theta_{\bar{f}_{4}})\cos\phi_{\bar{f}_{4}}$$

$$- (1-4\cos\theta_{f_{1}})\sin\phi_{f_{1}}(1-4\cos\theta_{\bar{f}_{4}})\sin\phi_{\bar{f}_{4}})$$

$$Im\left(\rho_{0+-0}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{-32}{9\pi^{2}}((1-4\cos\theta_{f_{1}})\cos\phi_{f_{1}}(1-4\cos\theta_{\bar{f}_{4}})\sin\phi_{\bar{f}_{4}}$$

$$+ (1-4\cos\theta_{f_{1}})\sin\phi_{f_{1}}(1-4\cos\theta_{\bar{f}_{4}})\cos\phi_{\bar{f}_{4}})$$

$$Re\left(\rho_{0+--}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{-4}{3\pi\sqrt{2}}(1-4\cos\... ...\cos\phi_{f_{1}}(5\cos^{2}\theta_{\bar{f}_{4}} - 2\cos\theta_{\bar{f}_{4}} - 1)$$

$$Im\left(\rho_{0+--}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{-4}{3\pi\sqrt{2}}(1-4\cos\... ...\cos\phi_{f_{1}}(5\cos^{2}\theta_{\bar{f}_{4}} - 2\cos\theta_{\bar{f}_{4}} - 1)$$

$$Re\left(\rho_{00++}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{1}{2}(2-5\cos^{2}\theta_{f_{1}})(5\cos^{2}\theta_{\bar{f}_{4}} + 2\cos\theta_{\bar{f}_{4}} - 1)$$

$$Im\left(\rho_{00++}(k)\right) =$$ 0

$$Re\left(\rho_{00+0}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{8}{3\pi\sqrt{2}}(2-5\cos^{2}\theta_{f_{1}})(1+4\cos\theta_{\bar{f}_{4}})\cos\phi_{\bar{f}_{4}}$$

$$Im\left(\rho_{00+0}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{-8}{3\pi\sqrt{2}}(2-5\cos^{2}\theta_{f_{1}})(1+4\cos\theta_{\bar{f}_{4}})\sin\phi_{\bar{f}_{4}}$$

$$Re\left(\rho_{00+-}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}2(2-5\cos^{2}\theta_{f_{1}})\cos2\phi_{\bar{f}_{4}}$$

$$Im\left(\rho_{00+-}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}-2(2-5\cos^{2}\theta_{f_{1}})\sin2\phi_{\bar{f}_{4}}$$

$$Re\left(\rho_{000+}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{8}{3\pi\sqrt{2}}(2-5\cos^{2}\theta_{f_{1}})(1+4\cos\theta_{\bar{f}_{4}})\cos\phi_{\bar{f}_{4}}$$

$$Im\left(\rho_{000+}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{8}{3\pi\sqrt{2}}(2-5\cos^{2}\theta_{f_{1}})(1+4\cos\theta_{\bar{f}_{4}})\sin\phi_{\bar{f}_{4}}$$

$$Re\left(\rho_{0000}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}(2-5\cos^{2}\theta_{f_{1}})(2-5\cos^{2}\theta_{\bar{f}_{4}})$$

$$Im\left(\rho_{0000}(k)\right) =$$ 0

$$Re\left(\rho_{000-}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{8}{3\pi\sqrt{2}}(2-5\cos^{2}\theta_{f_{1}})(1-4\cos\theta_{\bar{f}_{4}})\cos\phi_{\bar{f}_{4}}$$

$$Im\left(\rho_{000-}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{-8}{3\pi\sqrt{2}}(2-5\cos^{2}\theta_{f_{1}})(1-4\cos\theta_{\bar{f}_{4}})\sin\phi_{\bar{f}_{4}}$$

$$Re\left(\rho_{00-+}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}2(2-5\cos^{2}\theta_{f_{1}})\cos2\phi_{\bar{f}_{4}}$$

$$Im\left(\rho_{00-+}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}2(2-5\cos^{2}\theta_{f_{1}})\sin2\phi_{\bar{f}_{4}}$$

$$Re\left(\rho_{00-0}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{8}{3\pi\sqrt{2}}(2-5\cos^{2}\theta_{f_{1}})(1-4\cos\theta_{\bar{f}_{4}})\cos\phi_{\bar{f}_{4}}$$

$$Im\left(\rho_{00-0}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{8}{3\pi\sqrt{2}}(2-5\cos^{2}\theta_{f_{1}})(1-4\cos\theta_{\bar{f}_{4}})\sin\phi_{\bar{f}_{4}}$$

$$Re\left(\rho_{00--}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{1}{2}(2-5\cos^{2}\theta_{f_{1}})(5\cos^{2}\theta_{\bar{f}_{4}} - 2\cos\theta_{\bar{f}_{4}} - 1)$$

$$Im\left(\rho_{00--}(k)\right) =$$ 0

$$Re\left(\rho_{0-++}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{-4}{3\pi\sqrt{2}}(1+4\cos\... ...\cos\phi_{f_{1}}(5\cos^{2}\theta_{\bar{f}_{4}} + 2\cos\theta_{\bar{f}_{4}} - 1)$$

$$Im\left(\rho_{0-++}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{4}{3\pi\sqrt{2}}(1+4\cos\t... ...\sin\phi_{f_{1}}(5\cos^{2}\theta_{\bar{f}_{4}} + 2\cos\theta_{\bar{f}_{4}} - 1)$$

$$Re\left(\rho_{0-+0}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{-32}{9\pi^{2}}((1+4\cos\theta_{f_{1}})\cos\phi_{f_{1}}(1+4\cos\theta_{\bar{f}_{4}})\cos\phi_{\bar{f}_{4}}$$

$$- (1+4\cos\theta_{f_{1}})\sin\phi_{f_{1}}(1+4\cos\theta_{\bar{f}_{4}})\sin\phi_{\bar{f}_{4}})$$

$$Im\left(\rho_{0-+0}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{32}{9\pi^{2}}((1+4\cos\theta_{f_{1}})\cos\phi_{f_{1}}(1+4\cos\theta_{\bar{f}_{4}})\sin\phi_{\bar{f}_{4}}$$

$$+ (1+4\cos\theta_{f_{1}})\sin\phi_{f_{1}}(1+4\cos\theta_{\bar{f}_{4}})\cos\phi_{\bar{f}_{4}})$$

$$Re\left(\rho_{0-+-}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{-8\sqrt{2}}{3\pi}((1+4\cos\theta_{f_{1}})\cos\phi_{f_{1}}\cos2\phi_{\bar{f}_{4}}$$

$$- (1+4\cos\theta_{f_{1}})\sin\phi_{f_{1}}\sin2\phi_{\bar{f}_{4}})$$

$$Im\left(\rho_{0-+-}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{8\sqrt{2}}{3\pi}((1+4\cos\theta_{f_{1}})\cos\phi_{f_{1}}\sin2\phi_{\bar{f}_{4}}$$

$$+ (1+4\cos\theta_{f_{1}})\sin\phi_{f_{1}}\cos2\phi_{\bar{f}_{4}})$$

$$Re\left(\rho_{0-0+}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{-32}{9\pi^{2}}((1+4\cos\theta_{f_{1}})\cos\phi_{f_{1}}(1+4\cos\theta_{\bar{f}_{4}})\cos\phi_{\bar{f}_{4}}$$

$$+ (1+4\cos\theta_{f_{1}})\sin\phi_{f_{1}}(1+4\cos\theta_{\bar{f}_{4}})\sin\phi_{\bar{f}_{4}})$$

$$Im\left(\rho_{0-0+}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{-32}{9\pi^{2}}((1+4\cos\theta_{f_{1}})\cos\phi_{f_{1}}(1+4\cos\theta_{\bar{f}_{4}})\sin\phi_{\bar{f}_{4}}$$

$$- (1+4\cos\theta_{f_{1}})\sin\phi_{f_{1}}(1+4\cos\theta_{\bar{f}_{4}})\cos\phi_{\bar{f}_{4}})$$

$$Re\left(\rho_{0-00}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{-8}{3\pi\sqrt{2}}(1+4\cos\theta_{f_{1}})\cos\phi_{f_{1}}(2-5\cos^{2}\theta_{\bar{f}_{4}})$$

$$Im\left(\rho_{0-00}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{8}{3\pi\sqrt{2}}(1+4\cos\theta_{f_{1}})\sin\phi_{f_{1}}(2-5\cos^{2}\theta_{\bar{f}_{4}})$$

$$Re\left(\rho_{0-0-}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{-32}{9\pi^{2}}((1+4\cos\theta_{f_{1}})\cos\phi_{f_{1}}(1-4\cos\theta_{\bar{f}_{4}})\cos\phi_{\bar{f}_{4}}$$

$$- (1+4\cos\theta_{f_{1}})\sin\phi_{f_{1}}(1-4\cos\theta_{\bar{f}_{4}})\sin\phi_{\bar{f}_{4}})$$

$$Im\left(\rho_{0-0-}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{32}{9\pi^{2}}((1+4\cos\theta_{f_{1}})\cos\phi_{f_{1}}(1-4\cos\theta_{\bar{f}_{4}})\sin\phi_{\bar{f}_{4}}$$

$$+ (1+4\cos\theta_{f_{1}})\sin\phi_{f_{1}}(1-4\cos\theta_{\bar{f}_{4}})\cos\phi_{\bar{f}_{4}})$$

$$Re\left(\rho_{0--+}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{-8\sqrt{2}}{3\pi}((1+4\cos\theta_{f_{1}})\cos\phi_{f_{1}}\cos2\phi_{\bar{f}_{4}}$$

$$+ (1+4\cos\theta_{f_{1}})\sin\phi_{f_{1}}\sin2\phi_{\bar{f}_{4}})$$

$$Im\left(\rho_{0--+}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{-8\sqrt{2}}{3\pi}((1+4\cos\theta_{f_{1}})\cos\phi_{f_{1}}\sin2\phi_{\bar{f}_{4}}$$

$$- (1+4\cos\theta_{f_{1}})\sin\phi_{f_{1}}\cos2\phi_{\bar{f}_{4}})$$

$$Re\left(\rho_{0--0}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{-32}{9\pi^{2}}((1+4\cos\theta_{f_{1}})\cos\phi_{f_{1}}(1-4\cos\theta_{\bar{f}_{4}})\cos\phi_{\bar{f}_{4}}$$

$$+ (1+4\cos\theta_{f_{1}})\sin\phi_{f_{1}}(1-4\cos\theta_{\bar{f}_{4}})\sin\phi_{\bar{f}_{4}})$$

$$Im\left(\rho_{0--0}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{-32}{9\pi^{2}}((1+4\cos\theta_{f_{1}})\cos\phi_{f_{1}}(1-4\cos\theta_{\bar{f}_{4}})\sin\phi_{\bar{f}_{4}}$$

$$- (1+4\cos\theta_{f_{1}})\sin\phi_{f_{1}}(1-4\cos\theta_{\bar{f}_{4}})\cos\phi_{\bar{f}_{4}})$$

$$Re\left(\rho_{0---}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{-4}{3\pi\sqrt{2}}(1+4\cos\... ...\cos\phi_{f_{1}}(5\cos^{2}\theta_{\bar{f}_{4}} - 2\cos\theta_{\bar{f}_{4}} - 1)$$

$$Im\left(\rho_{0---}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{4}{3\pi\sqrt{2}}(1+4\cos\t... ...\sin\phi_{f_{1}}(5\cos^{2}\theta_{\bar{f}_{4}} - 2\cos\theta_{\bar{f}_{4}} - 1)$$

$$Re\left(\rho_{-+++}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\cos2\phi_{f_{1}}(5\cos^{2}\theta_{\bar{f}_{4}} + 2\cos\theta_{\bar{f}_{4}} - 1)$$

$$Im\left(\rho_{-+++}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\sin2\phi_{f_{1}}(5\cos^{2}\theta_{\bar{f}_{4}} + 2\cos\theta_{\bar{f}_{4}} - 1)$$

$$Re\left(\rho_{-++0}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{8\sqrt{2}}{3\pi}(\cos2\phi_{f_{1}}(1+4\cos\theta_{\bar{f}_{4}})\cos\phi_{\bar{f}_{4}}$$

$$+ \sin2\phi_{f_{1}}(1+4\cos\theta_{\bar{f}_{4}})\sin\phi_{\bar{f}_{4}})$$

$$Im\left(\rho_{-++0}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{-8\sqrt{2}}{3\pi}(\cos2\phi_{f_{1}}(1+4\cos\theta_{\bar{f}_{4}})\sin\phi_{\bar{f}_{4}}$$

$$- \sin2\phi_{f_{1}}(1+4\cos\theta_{\bar{f}_{4}})\cos\phi_{\bar{f}_{4}})$$

$$Re\left(\rho_{-++-}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}4(\cos2\phi_{f_{1}}\cos2\phi_{\bar{f}_{4}}+\sin2\phi_{f_{1}}\sin2\phi_{\bar{f}_{4}})$$

$$Im\left(\rho_{-++-}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}-4(\cos2\phi_{f_{1}}\sin2\phi_{\bar{f}_{4}}-\sin2\phi_{f_{1}}\cos2\phi_{\bar{f}_{4}})$$

$$Re\left(\rho_{-+0+}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{8\sqrt{2}}{3\pi}(\cos2\phi_{f_{1}}(1+4\cos\theta_{\bar{f}_{4}})\cos\phi_{\bar{f}_{4}}$$

$$- \sin2\phi_{f_{1}}(1+4\cos\theta_{\bar{f}_{4}})\sin\phi_{\bar{f}_{4}})$$

$$Im\left(\rho_{-+0+}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{8\sqrt{2}}{3\pi}(\cos2\phi_{f_{1}}(1+4\cos\theta_{\bar{f}_{4}})\sin\phi_{\bar{f}_{4}}$$

$$+ \sin2\phi_{f_{1}}(1+4\cos\theta_{\bar{f}_{4}})\cos\phi_{\bar{f}_{4}})$$

$$Re\left(\rho_{-+00}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}2\cos2\phi_{f_{1}}(2-5\cos^{2}\theta_{\bar{f}_{4}})$$

$$Im\left(\rho_{-+00}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}2\sin2\phi_{f_{1}}(2-5\cos^{2}\theta_{\bar{f}_{4}})$$

$$Re\left(\rho_{-+0-}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{8\sqrt{2}}{3\pi}(\cos2\phi_{f_{1}}(1-4\cos\theta_{\bar{f}_{4}})\cos\phi_{\bar{f}_{4}}$$

$$+ \sin2\phi_{f_{1}}(1-4\cos\theta_{\bar{f}_{4}})\sin\phi_{\bar{f}_{4}})$$

$$Im\left(\rho_{-+0-}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{-8\sqrt{2}}{3\pi}(\cos2\phi_{f_{1}}(1-4\cos\theta_{\bar{f}_{4}})\sin\phi_{\bar{f}_{4}}$$

$$- \sin2\phi_{f_{1}}(1-4\cos\theta_{\bar{f}_{4}})\cos\phi_{\bar{f}_{4}})$$

$$Re\left(\rho_{-+-+}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}4(\cos2\phi_{f_{1}}\cos2\phi_{\bar{f}_{4}}- \sin2\phi_{f_{1}}\sin2\phi_{\bar{f}_{4}})$$

$$Im\left(\rho_{-+-+}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}4(\cos2\phi_{f_{1}}\sin2\phi_{\bar{f}_{4}}+\sin2\phi_{f_{1}}\cos2\phi_{\bar{f}_{4}})$$

$$Re\left(\rho_{-+-0}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{8\sqrt{2}}{3\pi}(\cos2\phi_{f_{1}}(1-4\cos\theta_{\bar{f}_{4}})\cos\phi_{\bar{f}_{4}}$$

$$- \sin2\phi_{f_{1}}(1-4\cos\theta_{\bar{f}_{4}})\sin\phi_{\bar{f}_{4}})$$

$$Im\left(\rho_{-+-0}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{8\sqrt{2}}{3\pi}(\cos2\phi_{f_{1}}(1-4\cos\theta_{\bar{f}_{4}})\sin\phi_{\bar{f}_{4}}$$

$$+ \sin2\phi_{f_{1}}(1-4\cos\theta_{\bar{f}_{4}})\cos\phi_{\bar{f}_{4}})$$

$$Re\left(\rho_{-+--}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{1}{2}\cos2\phi_{f_{1}}(5\cos^{2}\theta_{\bar{f}_{4}} - 2\cos\theta_{\bar{f}_{4}} - 1)$$

$$Im\left(\rho_{-+--}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{1}{2}\sin2\phi_{f_{1}}(5\cos^{2}\theta_{\bar{f}_{4}} - 2\cos\theta_{\bar{f}_{4}} - 1)$$

$$Re\left(\rho_{-0++}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{-4}{3\pi\sqrt{2}}(1+4\cos\... ...\cos\phi_{f_{1}}(5\cos^{2}\theta_{\bar{f}_{4}} + 2\cos\theta_{\bar{f}_{4}} - 1)$$

$$Im\left(\rho_{-0++}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{-4}{3\pi\sqrt{2}}(1+4\cos\... ...\cos\phi_{f_{1}}(5\cos^{2}\theta_{\bar{f}_{4}} + 2\cos\theta_{\bar{f}_{4}} - 1)$$

$$Re\left(\rho_{-0+0}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{-32}{9\pi^{2}}((1+4\cos\theta_{f_{1}})\cos\phi_{f_{1}}(1+4\cos\theta_{\bar{f}_{4}})\cos\phi_{\bar{f}_{4}}$$

$$+ (1+4\cos\theta_{f_{1}})\sin\phi_{f_{1}}(1+4\cos\theta_{\bar{f}_{4}})\sin\phi_{\bar{f}_{4}})$$

$$Im\left(\rho_{-0+0}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{32}{9\pi^{2}}((1+4\cos\theta_{f_{1}})\cos\phi_{f_{1}}(1+4\cos\theta_{\bar{f}_{4}})\sin\phi_{\bar{f}_{4}}$$

$$- (1+4\cos\theta_{f_{1}})\sin\phi_{f_{1}}(1+4\cos\theta_{\bar{f}_{4}})\cos\phi_{\bar{f}_{4}})$$

$$Re\left(\rho_{-0+-}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{-8\sqrt{2}}{3\pi}((1+4\cos\theta_{f_{1}})\cos\phi_{f_{1}}\cos2\phi_{\bar{f}_{4}}$$

$$+ (1+4\cos\theta_{f_{1}})\sin\phi_{f_{1}}\sin2\phi_{\bar{f}_{4}})$$

$$Im\left(\rho_{-0+-}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{8\sqrt{2}}{3\pi}((1+4\cos\theta_{f_{1}})\cos\phi_{f_{1}}\sin2\phi_{\bar{f}_{4}}$$

$$- (1+4\cos\theta_{f_{1}})\sin\phi_{f_{1}}\cos2\phi_{\bar{f}_{4}})$$

$$Re\left(\rho_{-00+}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{-32}{9\pi^{2}}((1+4\cos\theta_{f_{1}})\cos\phi_{f_{1}}(1+4\cos\theta_{\bar{f}_{4}})\cos\phi_{\bar{f}_{4}}$$

$$- (1+4\cos\theta_{f_{1}})\sin\phi_{f_{1}}(1+4\cos\theta_{\bar{f}_{4}})\sin\phi_{\bar{f}_{4}})$$

$$Im\left(\rho_{-00+}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{-32}{9\pi^{2}}((1+4\cos\theta_{f_{1}})\cos\phi_{f_{1}}(1+4\cos\theta_{\bar{f}_{4}})\sin\phi_{\bar{f}_{4}}$$

$$+ (1+4\cos\theta_{f_{1}})\sin\phi_{f_{1}}(1+4\cos\theta_{\bar{f}_{4}})\cos\phi_{\bar{f}_{4}})$$

$$Re\left(\rho_{-000}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{-8}{3\pi\sqrt{2}}(1+4\cos\theta_{f_{1}})\cos\phi_{f_{1}}(2-5\cos^{2}\theta_{\bar{f}_{4}})$$

$$Im\left(\rho_{-000}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{-8}{3\pi\sqrt{2}}(1+4\cos\theta_{f_{1}})\sin\phi_{f_{1}}(2-5\cos^{2}\theta_{\bar{f}_{4}})$$

$$Re\left(\rho_{-00-}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{-32}{9\pi^{2}}((1+4\cos\theta_{f_{1}})\cos\phi_{f_{1}}(1-4\cos\theta_{\bar{f}_{4}})\cos\phi_{\bar{f}_{4}}$$

$$+ (1+4\cos\theta_{f_{1}})\sin\phi_{f_{1}}(1-4\cos\theta_{\bar{f}_{4}})\sin\phi_{\bar{f}_{4}})$$

$$Im\left(\rho_{-00-}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{32}{9\pi^{2}}((1+4\cos\theta_{f_{1}})\cos\phi_{f_{1}}(1-4\cos\theta_{\bar{f}_{4}})\sin\phi_{\bar{f}_{4}}$$

$$- (1+4\cos\theta_{f_{1}})\sin\phi_{f_{1}}(1-4\cos\theta_{\bar{f}_{4}})\cos\phi_{\bar{f}_{4}})$$

$$Re\left(\rho_{-0-+}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{-8\sqrt{2}}{3\pi}((1+4\cos\theta_{f_{1}})\cos\phi_{f_{1}}\cos2\phi_{\bar{f}_{4}}$$

$$- (1+4\cos\theta_{f_{1}})\sin\phi_{f_{1}}\sin2\phi_{\bar{f}_{4}})$$

$$Im\left(\rho_{-0-+}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{-8\sqrt{2}}{3\pi}((1+4\cos\theta_{f_{1}})\cos\phi_{f_{1}}\sin2\phi_{\bar{f}_{4}}$$

$$+ (1+4\cos\theta_{f_{1}})\sin\phi_{f_{1}}\cos2\phi_{\bar{f}_{4}})$$

$$Re\left(\rho_{-0-0}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{-32}{9\pi^{2}}((1+4\cos\theta_{f_{1}})\cos\phi_{f_{1}}(1-4\cos\theta_{\bar{f}_{4}})\cos\phi_{\bar{f}_{4}}$$

$$- (1+4\cos\theta_{f_{1}})\sin\phi_{f_{1}}(1-4\cos\theta_{\bar{f}_{4}})\sin\phi_{\bar{f}_{4}})$$

$$Im\left(\rho_{-0-0}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{-32}{9\pi^{2}}((1+4\cos\theta_{f_{1}})\cos\phi_{f_{1}}(1-4\cos\theta_{\bar{f}_{4}})\sin\phi_{\bar{f}_{4}}$$

$$+ (1+4\cos\theta_{f_{1}})\sin\phi_{f_{1}}(1-4\cos\theta_{\bar{f}_{4}})\cos\phi_{\bar{f}_{4}})$$

$$Re\left(\rho_{-0--}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{-4}{3\pi\sqrt{2}}(1+4\cos\... ...\cos\phi_{f_{1}}(5\cos^{2}\theta_{\bar{f}_{4}} - 2\cos\theta_{\bar{f}_{4}} - 1)$$

$$Im\left(\rho_{-0--}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{-4}{3\pi\sqrt{2}}(1+4\cos\... ...\cos\phi_{f_{1}}(5\cos^{2}\theta_{\bar{f}_{4}} - 2\cos\theta_{\bar{f}_{4}} - 1)$$

$$Re\left(\rho_{--++}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{1}{4}(5\cos^{2}\theta_{f_{... ...eta_{f_{1}} - 1)(5\cos^{2}\theta_{\bar{f}_{4}} + 2\cos\theta_{\bar{f}_{4}} - 1)$$

$$Im\left(\rho_{--++}(k)\right) =$$ 0

$$Re\left(\rho_{--+0}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{4}{3\pi\sqrt{2}}(5\cos^{2}... ...} - 2\cos\theta_{f_{1}} - 1)(1+4\cos\theta_{\bar{f}_{4}})\cos\phi_{\bar{f}_{4}}$$

$$Im\left(\rho_{--+0}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{-4}{3\pi\sqrt{2}}(5\cos^{2... ...} + 2\cos\theta_{f_{1}} - 1)(1+4\cos\theta_{\bar{f}_{4}})\sin\phi_{\bar{f}_{4}}$$

$$Re\left(\rho_{--+-}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}(5\cos^{2}\theta_{f_{1}} + 2\cos\theta_{f_{1}} - 1)\cos2\phi_{\bar{f}_{4}}$$

$$Im\left(\rho_{--+-}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}-(5\cos^{2}\theta_{f_{1}} + 2\cos\theta_{f_{1}} - 1)\sin2\phi_{\bar{f}_{4}}$$

$$Re\left(\rho_{--0+}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{4}{3\pi\sqrt{2}}(5\cos^{2}... ...} - 2\cos\theta_{f_{1}} - 1)(1+4\cos\theta_{\bar{f}_{4}})\cos\phi_{\bar{f}_{4}}$$

$$Im\left(\rho_{--0+}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{4}{3\pi\sqrt{2}}(5\cos^{2}... ...} - 2\cos\theta_{f_{1}} - 1)(1+4\cos\theta_{\bar{f}_{4}})\sin\phi_{\bar{f}_{4}}$$

$$Re\left(\rho_{--00}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{1}{2}(5\cos^{2}\theta_{f_{1}} + 2\cos\theta_{f_{1}} - 1)(2-5\cos^{2}\theta_{\bar{f}_{4}})$$

$$Im\left(\rho_{--00}(k)\right) =$$ 0

$$Re\left(\rho_{--0-}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{4}{3\pi\sqrt{2}}(5\cos^{2}... ...} - 2\cos\theta_{f_{1}} - 1)(1-4\cos\theta_{\bar{f}_{4}})\cos\phi_{\bar{f}_{4}}$$

$$Im\left(\rho_{--0-}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{-4}{3\pi\sqrt{2}}(5\cos^{2... ...} - 2\cos\theta_{f_{1}} - 1)(1-4\cos\theta_{\bar{f}_{4}})\sin\phi_{\bar{f}_{4}}$$

$$Re\left(\rho_{---+}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}(5\cos^{2}\theta_{f_{1}} + 2\cos\theta_{f_{1}} - 1)\cos2\phi_{\bar{f}_{4}}$$

$$Im\left(\rho_{---+}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}(5\cos^{2}\theta_{f_{1}} + 2\cos\theta_{f_{1}} - 1)\sin2\phi_{\bar{f}_{4}}$$

$$Re\left(\rho_{---0}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{4}{3\pi\sqrt{2}}(5\cos^{2}... ...} - 2\cos\theta_{f_{1}} - 1)(1-4\cos\theta_{\bar{f}_{4}})\cos\phi_{\bar{f}_{4}}$$

$$Im\left(\rho_{---0}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{4}{3\pi\sqrt{2}}(5\cos^{2}... ...} - 2\cos\theta_{f_{1}} - 1)(1-4\cos\theta_{\bar{f}_{4}})\sin\phi_{\bar{f}_{4}}$$

$$Re\left(\rho_{----}(k)\right) = \frac{1}{N_{k}}\sum_{i=1}^{N_{k}}\frac{1}{4}(5\cos^{2}\theta_{f_{... ...eta_{f_{1}} - 1)(5\cos^{2}\theta_{\bar{f}_{4}} - 2\cos\theta_{\bar{f}_{4}} - 1)$$

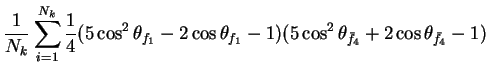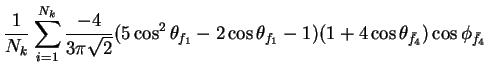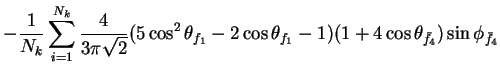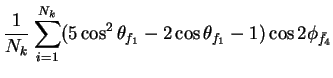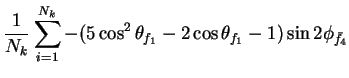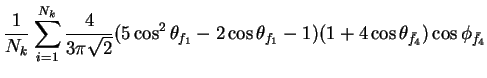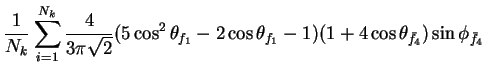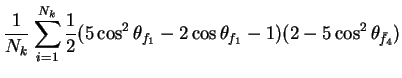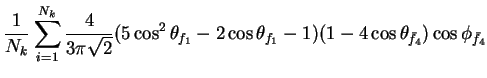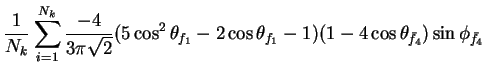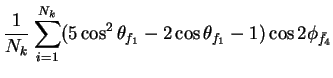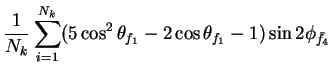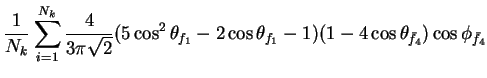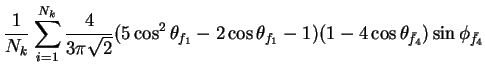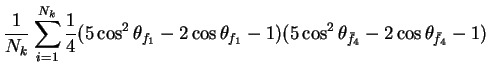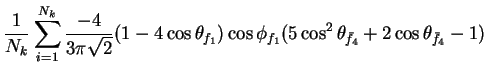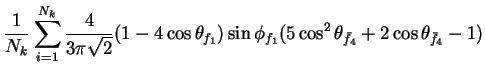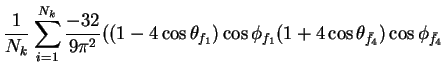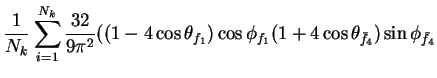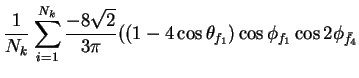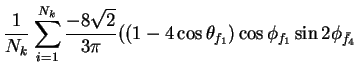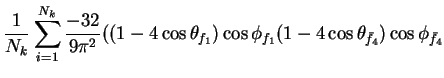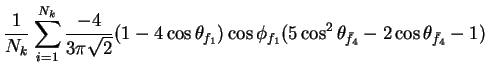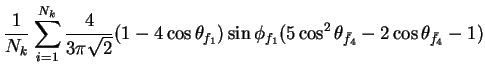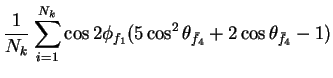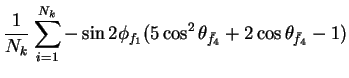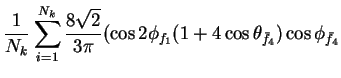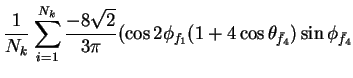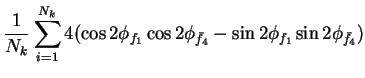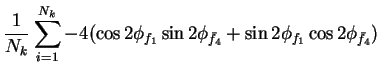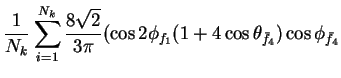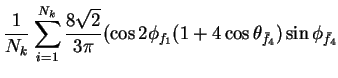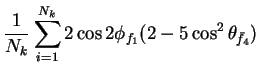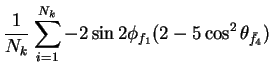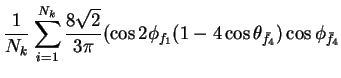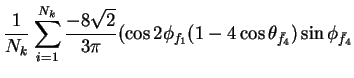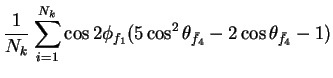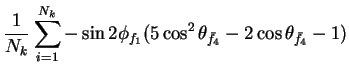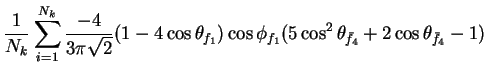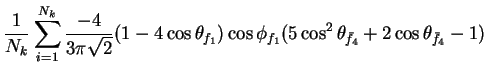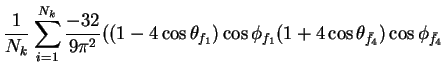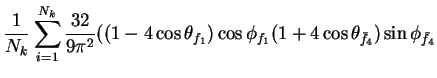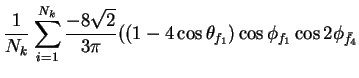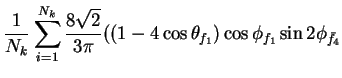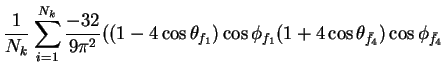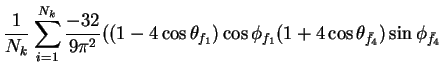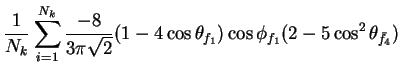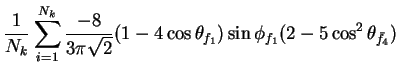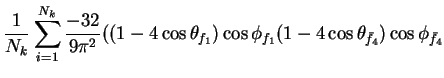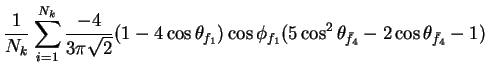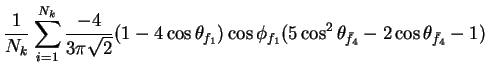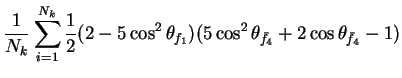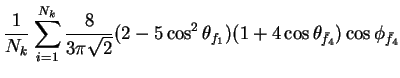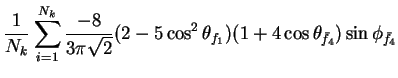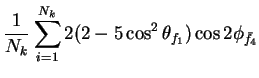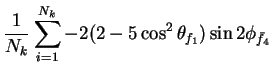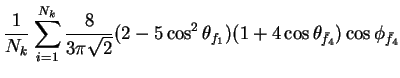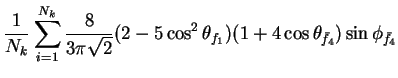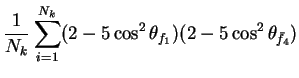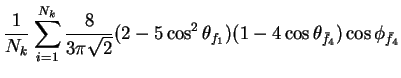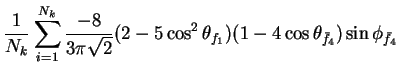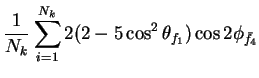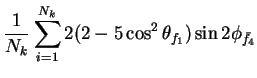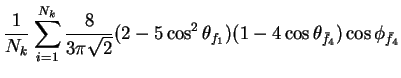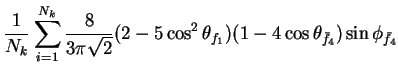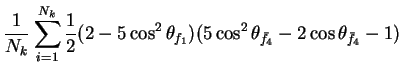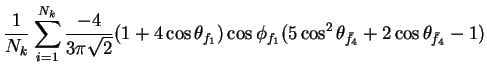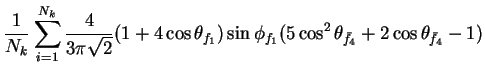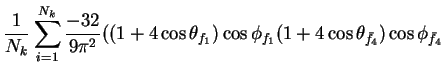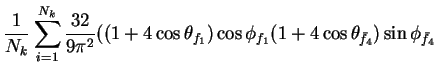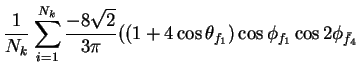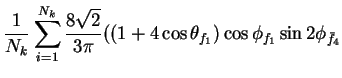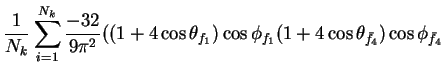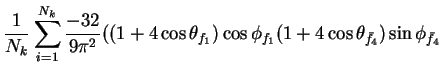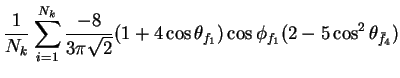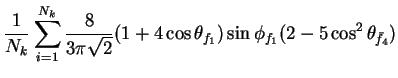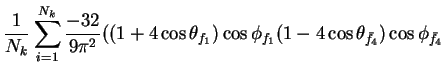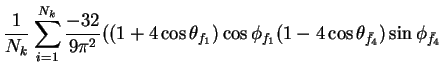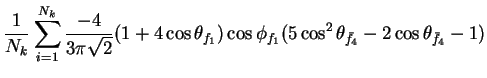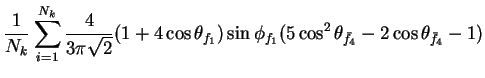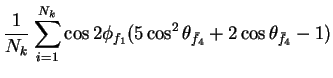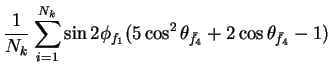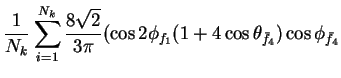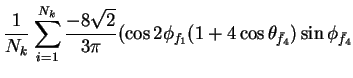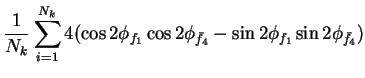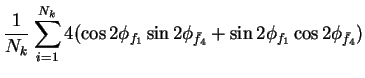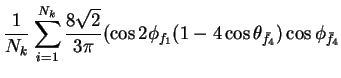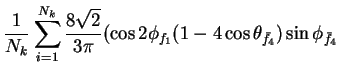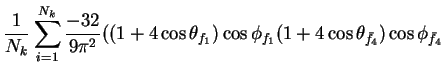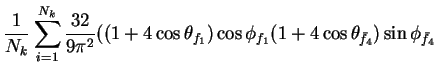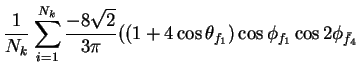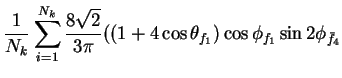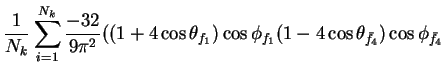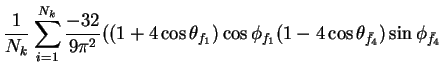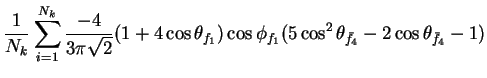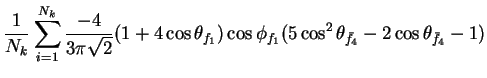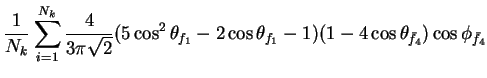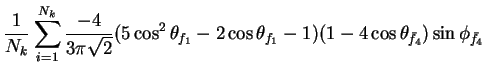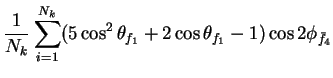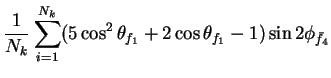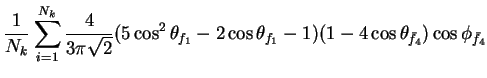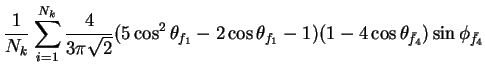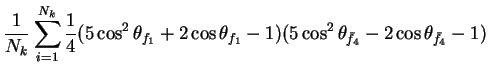$$Im\left(\rho_{----}(k)\right) =$$ 0