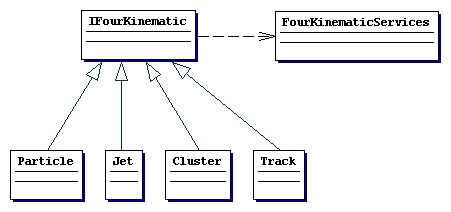
If we decide that all of Particle, Jet, Cluster and Track should honour this interface then the simple class relation diagram given below results:
P.Clarke, M.Dobbs, H.Phillips, D.Rousseau, P.Sherwood
There are many benefits which may be obtained by doing this ranging from standardisation of accessor names across ATLAS to the use of generic algorithms which can make code much more compact and reliable. More than this, there should be a long terms gain through the better structure of programs which results from adhering to the philosophy of "programming to interfaces" and not to "specific concrete classes".
We assume that the reader is familiar with the concept of an "interface". To be specific in C++ we mean the use of "pure virtual abstract base classes". The concept is so important that in Java it has been formalised by distinguishing intefaces from implementation classes by the use of the keyword "interface" itself.
The document makes some suggestions for interface structures ranging
from the most simple to the more complicated.
However we emphasise here and elsewhere in the document that
it is fully recognised that the detailed content of such interfaces requires
agreement of a wide range of people involved in simulation and reconstruction.
The authors are proposing only a general structure, and do not in any way
imply that they know all of the correct attributes, not to limit the information
that experts in particular areas (eg tracking, cluster building) deem necessary
to be included in any concrete class, or indeed in specialist interfaces.
IThreeKinematic and IFourKinematic interfaces
Appendix: Examples of use of IKinematic
We assume that the reader is already familiar with the concept of interfaces. To those already familiar with OO programming, particularly Java, this will likely be the case. For those who are not (there is unfortunately no equivalent in FORTRAN) we reccommend the book "Scientific and Enginerring C++" by Barton&Nachman ISBN:0-201-53393-6 which covers this in great detail. The briefest summary is given here, and more will become clear in the next section.
An interface is a way of formally requiring a set of method signatures
(by a special sort of class inheritance), without actually specifiying
the code to implement the methods. In general several concrete classes
will then honour such an interface. They are free to implement the actual
code needed for each method in any way they wish. Such code can be different
in each case and implemented well after defining the interface. Client
code can then use concrete objects via their interface type and not the
concrete object type itself. Thus analysis code can be written which is
independent ofconcrete types and which will therefore work on a whole range
of objects, including ones which have not yet been invented. This is potentially
very powerful. We list some of the motivations:
Particle
particle ;
Jet
bjet ;
cout
<< " Eta of the particle is " << particle.eta(
) ;
cout
<< " Eta of the b-jet is " <<
bjet.eta( ) ;
This alone, trivial as it may seem, is almost enough to motivate the
use of an interface. Otherwise different authors will use eta(), Eta(),
eta0(), pseudoRapidity(), ....etc.. and it would always be necessary
to look up the specific name s used for each class. To put it another way,
it would be chaotic if the same kinematic quantitiy used throught ATLAS
had to be accessed in arbitrarily different ways.
Particle
p ;
Jet j ;
double
dr = helper.deltaR( j, p ) ;
where helper is
some helper class where the operation is coded. The method deltaR( ) would
work for any objects which honoured the interface.
Writing these function objects is technically very simple, but in practice
is not "intuitive" to the novice C++ programmer. However if all types
honour a kinematic interface, then it is possible to provide many of the
commonly needed function objects centrally, avoiding the need for users
to write them themselves. This is described more clearly below.
In all the following we will assume the following examples of concrete classes which might honour the interfces:
Particle
// represents electron, muon, phonton ...etc
Jet
// represents a jet
Cluster
// represents a calorimeter cluster
Track
// represents a track
[Note to the purists: The purist may say that this all looks a little
procedural. Really one should be asking what one wants to do with an entity,
and either implementing methods to do it in the entity itself, or defining
other classes to do the job. Worrying about exposing atomic bits of kinematic
information on the surface may therefore seem to have missed the point
of OO. However since ATLAS has adopted an approach which seeks to
seperate "data" objects from "algorithmic" objects then this is probably
not so bad. Also, whatever debate one may have, we take it as axiomatic
that a large group of physicist users would consider it obtuse to be denied
access to quantities like eta and phi directly.]
This is the briefest introduction to interfaces for the novice. Please however consult the standard C++ books for more explicit detail.
To provide an interface means writing a special class which defines only method names, but does not actually provide any code. For example suppose we want an interface to define methods to access eta and phi only. We write
class
IDirection {
public:
virtual double eta( ) = 0;
virtual double phi( ) = 0;
}
;
This interface is called IDirection (we adopt the Gaudi convention of starting interfaces with an I....). It promises that there will be two methods, giving their unambiguous signatures. The =0 is important. This says that there is not going to be any code provided anywhere for the IDirection class itself.
Now if we want to make two concrete classes, each of which will honour this interface, then we inherit it into each of them (we explain the virtual keyword later). Take Particle and Jet as examples:
class
Particle: virtual public IDirection {
public:
double eta( ) { return m_momentum.pseudoRapidity( ) ; }
double phi( ) { return m_momentum.phi( ) ; }
..... other declarations for this class
private:
HepLorenzVector m_momentum ;
};
class
Jet: virtual public IDirection {
public:
double eta( ) { return m_eta ; }
double phi( ) { return m_phi ; }
..... other declarations for this class
private:
double m_eta ;
double m_phi ;
};
Each concrete class now provides code to implement the eta( ) and phi( ) methods. Note that they choose to do it differently. This is fine, the implementation is not constrained, only that eta( ) returns a double ...etc. The writers of Particle and Jet are obliged to provide these methods with these names., but they can do it as they like This is a key point !.
Thus the minimum achieved so far is that everyone knows that to get eta or phi from either type you use these standardised method names.
More useful is that we can now use either of Particle or Jet as if it were an IDirection. Here is a function which is written to operate on IDirection types. It calculates the difference in eta between twom operands. It doesnt know anything about Particles, Jets, in fact they neednt have been invented at the time of writing the function.
double
deltaEta( IDirection& first, IDirection& second )
{
return first.eta( ) - second.eta( ) ;
}
Here is some user code to demonstrate use of the function:
Particle
p ;
Jet
j ;
cout
<< " The eta difference between particle and jet is " <<
deltaEta( p, j ) ;
[Note: for those familiar with the work done on Atlfast, this is essentially IKinematic with some additions]
This is motivated by the practical observation that for much analysis there are many kinematic operations for which the user will want to view Particles, Jets, Clusters, and Tracks in the same way: i.e as an object which has four-momentum like kinematic attributes.
Let us call this interface IFourKinematic Some methods which could be promised by the IFourKinematic interface are detailed in the table below.
The reader will see that apart from the obvious momentum attributes, the concept of "point of definition" is included. This was felt to be necessary due to the variable production point of LHC events (particularly in z). Without this there would be an implicit assumption that the momentum attributes were measured at the origin. In some cases this would be an approximation, in others wrong. Without this information it would then be impossible to form an invariant mass or to use the information for "closeness" matching.
The set is neither exhaustive not mandatory. In particular several of the authors come form LEP and therefore have a rose tinted spectacle view of attributes which might be useful in a hadronic environment ?
Important note: The reader should NOT get hung up on methods or their names. The point of the document is primarily to motivate the adoption of an appropriate hierarchy of interfaces. The exact methods and their names can be decided later following coding rules , prejudice and common agreement.
| IFourKinematic interface | ||
| Return type | method name | description |
| Direction quantitites | ||
| double | eta( ) | eta coordinate of centroid of entity |
| double | phi( ) | phi coordinate of centroid of entity |
| double | cosTheta( ) | cosine of theta |
| Total quantities | ||
| double | energy( ) | energy |
| double | pmag( ) | magnitude of three-momentum |
| double | mass( ) | mass |
| Transverse quantities | ||
| double | e_t( ) | transverse energy |
| double | p_t( ) | transverse momentum |
| double | m_t( ) | transverse mass |
| Cartesian quantitites | ||
| double | p_x( ) | x component of momentum |
| double | p_y( ) | y component |
| double | p_z( ) | z component |
| Momentum Vector quantities | ||
| HepLorentzVector | momentum( ) | full 4-momentum of the entity |
| HepLorentzVector | operator HepLorentzVector( ) | Conversion to HepLorentzVector |
| Point of of definition of momentum | ||
| Hep3Vector | pointOfDefinition( ) | 3-position at which 4-momentum is defined. |
Analysis entities should inherit this interface in the following way (shown for the Particle class):
class Particle: virtual public IFourKinematic ;
The virtual qualifier is required for technical reasons.
If we decide that all of Particle, Jet, Cluster and Track should
honour this interface then the simple class relation diagram given below
results:

If we were to stop here we would have to recognise that what we are
doing is wrong from a purist point of view. Some of the concrete classes
do not really have all the IFourKinematic attributes. Tracks only have
three-momentum attributes, and dont have energy or mass unless you hypothesise
them to be some specific particle.. Clusters have an energy and direction,
but don't have a three-momentum unless you hypothsise that they are
also some specific particle. We can of course chose sensible defaults
in order to do this: if we say that all tracks and clusters are assumed
to correspond to particles with zero mass then we can make up the missing
quantities.
Arguments for and against might be:
For:
- Its very simple and utileAgainst- Sensible defaults exist
- Its wrong. OO tells us it is short sighted to fudge something now just because you cant see a problem with it now. Later on this will come back and haunt you !.[The astute reader will realise at this point that the problem is arising purely because one is trying to use objects as sometying they are not. I.e using Tracks as Pions, or Clusters as Photons. We return to this point later.]- Everyone has to "remember" what to do when writing a concrete class.
- You can perform ill defined operations. For example finding deltaPhi between a Track and a Cluster for association reasons. A track direction is defined at the origin and must be adjusted for B-field deflection before it can be compared to a Cluster at the calorimeter surface. This tells you that the kinematic attributes of Clusters and Tracks are probably different types.
This interface was used extensively in the development of the new OO Athena-Atlfast (it was actually called IKinematic in that context). It certainly proved to be very useful, and would certainly be used by several of the authors in their own private analysis code if it were not provided centrally by ATLAS.
We could simply introduce distinct three-momentum and four-momentum interfaces. Call these IThreeKinematic and IFourKinematic respectively.
IFourKinematic inherits from IThreeKinematic
class IFourKinematic : virtual public IThreeKinematic {...};
and is identical to the previous section.
IThreeKinematic
interface methods are given in the table below. They are a subset
of IFourKinematic.
| IThreeKinematic | ||
| Return type | method name | description |
| Direction quantitites | ||
| double | eta( ) | eta coordinate of centroid of entity |
| double | phi( ) | phi coordinate of centroid of entity |
| double | cosTheta( ) | cosine of theta |
| Total quantities | ||
| double | pmag( ) | magnitude of three-momentum |
| Transverse quantities | ||
| double | p_t( ) | transverse momentum |
| Cartesian quantitites | ||
| double | p_x( ) | x component of momentum |
| double | p_y( ) | y component |
| double | p_z( ) | z component |
| Vector quantities | ||
| Hep3Vector | momentum( ) | full 3-momentum of the entity |
| Hep3Vector | operator Hep3Vector( ) | Conversion to Hep3Vector |
| Point of definition | ||
| Hep3Vector | pointOfDefinition( ) | 3-position at which 3-momentum defined. |
Particle, Jet and Track would appear as shown in the class relation diagram shown below. We have for now also shown Cluster using IThreeKinematic although this is not evidently really correct and will be discussed next.
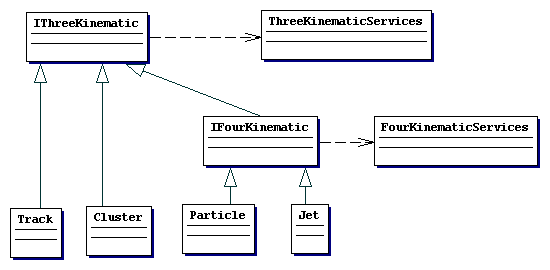
Using this structure the writer of a concrete Track class now only needs to provide the truly relevant method implementations. Utility code will be written to only use the appropriate interface. For example the function to calculate deltaEta would now look like this:
double
deltaEta( IThreeKinematic& first, IThreeKinematic& second )
{
return first.eta( ) - second.eta( ) ;
}
and would of course work for both IThreeKinematic and IFourKinematic objects passed as arguments due to the inheritance.
Arguments for and against this hierarchy might be
For:
- Appears to be more correct in the sense that more of the distinct types are treated in a more appropriate way.Against:- Utility code still easy to write because of interface inheritance
- Not particularly complicated.
- One could NOT now attempt to sort Tracks by, say, eT() or take their invariant mass without being specific about mass (some would see this as correct).
- Unnecessarily complicated.- One could not now attempt to sort Tracks by, say, eT() or take their invariant mass without being specific about mass (some would see this as a practical disadvantage).
- You can still perform ill defined operations. For example finding deltaPhi between a Track and a Cluster for association reasons. A track direction is defined at the origin and must be adjusted for B-field deflection before it can be compared to a Cluster at the calorimeter surface
- Clearly still wrong for Clusters where "energy-like " method names would be more intuitive.
In the last section we did not solve the problem of Cluster kinematics. Clusters are neither four-momentum like, nor are they truly a three-momentum. Also it would be obtuse to do away with methods like energy( ) or eT( ) for Clusters as would happen if they honoured only IThreeKinematic.
This tells you that you should consider a distinct Interface type for
Clusters (or in fact any energy deposit at a given space point" ). We call
this IEnergyDeposit
Possible IEnergyDeposit
methods are given in the table below.
| IEnergyDeposit | ||
| Return type | method name | description |
| Direction quantitites | ||
| double | eta( ) | eta coordinate of centroid of entity |
| double | phi( ) | phi coordinate of centroid of entity |
| double | cosTheta( ) | cosine of theta |
| Total quantities | ||
| double | energy( ) | magnitude of energy deposit. |
| Transverse "quantities" | ||
| double | e_t( ) | transverse energy defined in the customary way. |
| Cartesian "quantitites" | ||
| double | e_x( ) | x "component" of energy |
| double | e_y( ) | y "component "of energy |
| double | e_z( ) | z "component" of energy |
| Vector quantities | ||
| Hep3Vector | direction( ) | direction of Cluster from origin |
| Hep3Vector | position( ) | position of Cluster centroid w.r.t. origin |
Particle, Jet, Track and Cluster would appear as shown in the class relation diagram shown below.
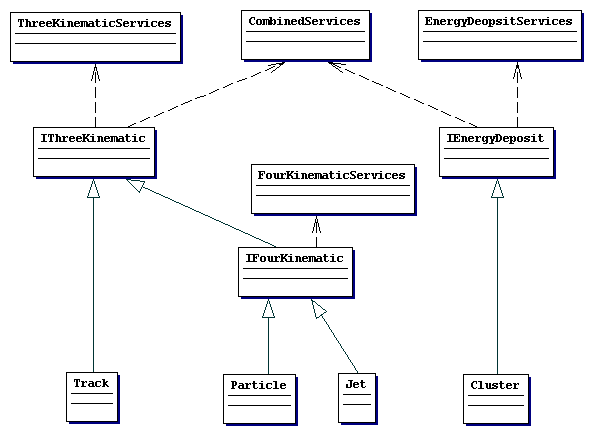
[Note: we have at this stage resisted the temptation to assume that this must necessarily be the "other part of IFourKinematic", i.e should be seen as the 4th part of a 4-momentum vector so that IFourKinematic would be made up simply by inheriting IThreeKinematic and IEnergyDeposit. This seems tempting but this is not really what IEnergyDeposit is. As presented here it represents an energy deposit at some centroid position. ]
Arguments for and against this hierarchy might be
For:
- Appears to be formally more correct.Against:- Utility code more complex to write as Clusters must be treated differently. This might be good because it forces the explicit acceptance early on that it truly is a different type.
- Less likely to perform ill defined operations, such as wrongly calculating a deltaPhi between a Track and a Cluster. Now you are forced to explicitly recognise that they are different and can therefore provide the correct overloaded implementation based upon the function argument type.
- Appears to be getting fairly complicated.At this point the underlying problem becomes manifest. We suggest it arises because it is too easy for physicists to equate (in their heads) the concept of "energy deposit at a point" with "hypothesised photon" or "hypothesised electron". A formal way to solve this would be to insist that Clusters are NOT used in this way. Instead the user shouold be required to be explicit about their hypothesis and promote the entity to the stauts of a particle. For example one way to do this would be to make the Particle class construct its self from Tracks and Clusters, i.e. something like:- Utility code more complex to write as Clusters must be treated differently. Some might think this loses a de-facto simplicity which is still there in practice.
Cluster c ;
Track t ;
Particle p1 ( c, mass, charge ) // must supply assumed mass
and assumed charge.
Particle p2 ( c, pdt_id ) // specify explicit pdg identifier
code
Particle p2 ( t, mass ) // a track already
has a charge
This may well overlap in spirit with the contents of the talk by Srini Rajagopalan given at the reconstruction workshop in October 2000. Here an new class "EMObject " is made from Clusters. EMObject contains some "value added" w.r.t Clusters, and would have IFourKinematic attributes.
Further discussion with SR & co is in order here before taking
this any further.
In this approach we consider each type independently and decide what
a sensible interface for kinematic quantities would be. I.e. in thinking
of Tracks we do not worry about Clusters ..etc.. . Only after performing
this step will we look to see how (if at all) a harmonisation of equivalent
attributes through an inheritance structure might be imposed.
Let us assume that
All concrete Particle classes will honour an IParticleKinematic interface
All concrete Jet classes will honour an IJetKinematic interface
All concrete Cluster classes will honour an IClusterKinematic interface
All concrete Track classes will honour an ITrackKinematic interfaceActually, this alone may be a very good thing to agree, regardless of whether commonality across these types can be found. It would go a long way toward ensuring that analysis code could work transparently upon many different concrete types. In other words ATLAS should not worry about pursuing commonality of concrete types, but instead pursue commonality of interfaces which those Tracks should honour.
In addition we assume that users would also want to see all of the attributes in IThreeKinematic. Therefore we assume ITrackKinematic to also inherit IThreeKinematic
We have looked at SimpleTrack which has recently been written as a stop-gap measure (Laurent Vacavant) whilst awaiting more sophisticated track classes to be developed. The main set of attributes included there but not show below are:
- An almost equivalent set pertaining to the end of the Track. These could easily be included.
- Radius of Bremsstrahlung. This could easily be included if it was truly part of kinematic information. Should be the subject of a use case study first however.
- Hit information. This should NOT be included in this interface as it is NOT kinematic information. It shoud instead be available through a construction tracing history scheme.
| ITrackKinematic:
virtual public IThreeKinematic |
||
| Return type | method name | description |
| Cannonical fitting quantities | ||
| double | dZero( ) | closest approach to the r-phi origin |
| double | zZero | z position at closest approach to r-phi origin |
| double | phi( ) | phi of track at closest approach |
| double | cotTheta( ) | co-tangent of theta at closest approach |
| double | inverseChargedPt( ) | Q* 1/pt |
| Correlation co-efficients | ||
| SquareMatrix<5> | correlation( ) | 5 x 5 correlation matrix. |
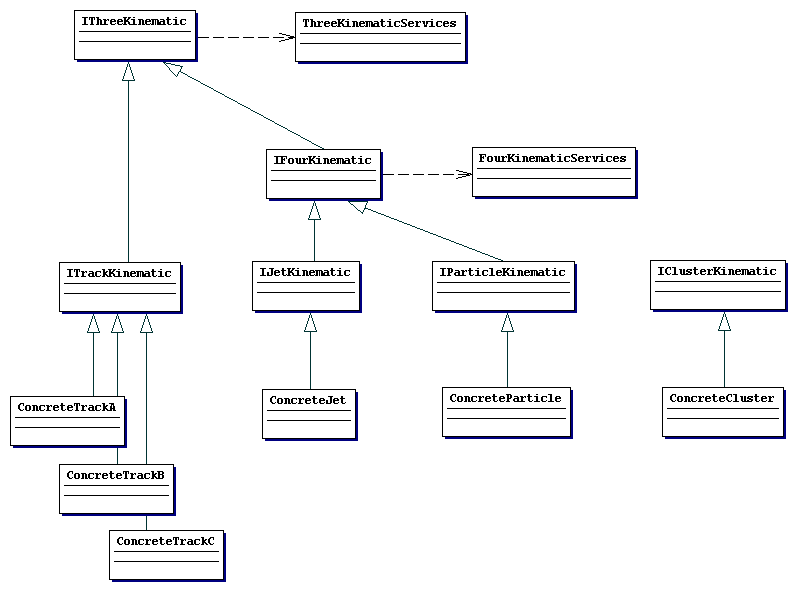
The scheme may look complicated, but this may just be an illusion. The correct question to ask is what complexity does any given user have to see to write their code.
- From the point of view of an "end of the chain analyst" most entities could be used via their specific interfaces ("front line" interfaces) which is the whole point of this approach. This would accrue all of the benefits of polymorphism in respect of different concrete types.
- An "analyst" would not need to know or care much about the inheritance structure behind the front line interfaces. Thus the apparent complexity would not be something they need to know about for the purposes of writing an analysis. They need only look at the methods promised in the front line interface.
- The behind the scenes inheritance could be used to enforce unique names for the same attributes, and provide common kinematic operations as mentioned at the beginning of this document.
- A user who needs to write something which needs to know about the inheritance structure is probably doing something for which they should have to know this anyway. To be verified via use cases.
We suggest that some serious though is given to the pros and cons of either:
Requiring users to make such hypotheses explicit in their code (by the use of Particles constructed from Clusters and Tracks)Accepting that "using a Track as a pion" and "using a Cluster as a photon" are so common that this should be possible without any extra complication. This equates to users not making this hypothesis explicit, but simply assuming that "we all remember it what will happen when mixing Clusters with Particles"
The next next steps are:
KinematicHelper : a helper class to encapsulate common functions needed on IKinematic types.
Function objects for use with STL algorithms (eg sort) : pre-defined function objects to help the user make use of the STL generic algorithms.
