 Fig
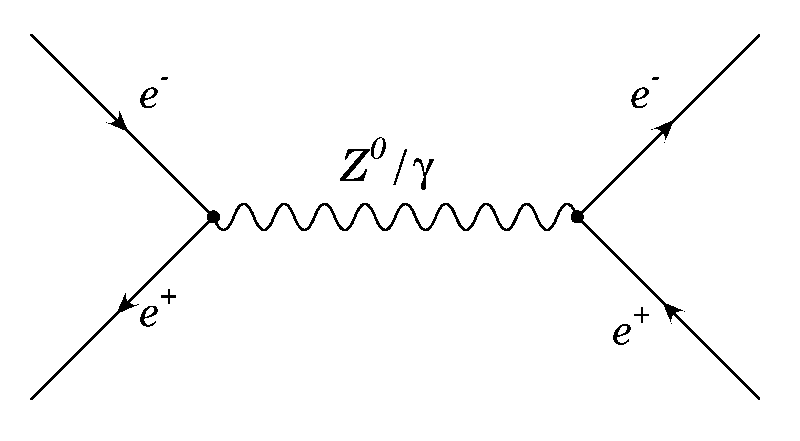
d: s-channel bhabha scattering-----Fig e: t-channel bhabha scattering
Fig
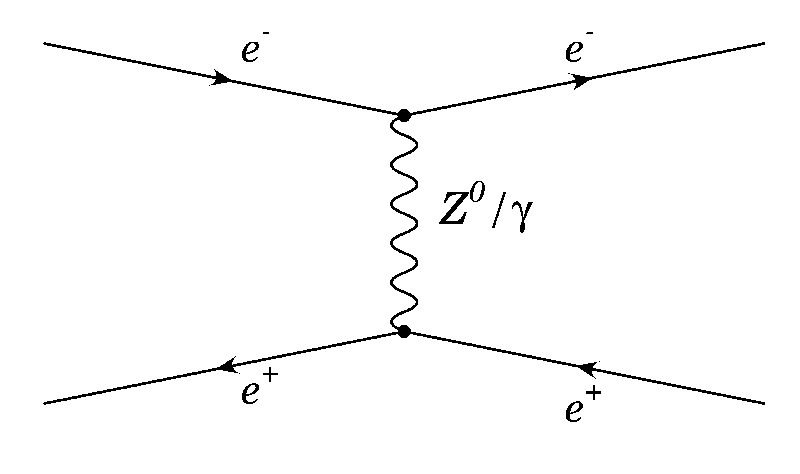
d: s-channel bhabha scattering-----Fig e: t-channel bhabha scattering
 Fig
d: s-channel bhabha scattering-----Fig e: t-channel bhabha scattering
Fig
d: s-channel bhabha scattering-----Fig e: t-channel bhabha scattering
To regain the accuracy lost from luminosity spectrum smearing in a e+e- collider, several methods are considered, using bhabha scattering events. In both cases, for a given event where a photon was radiated the true center of mass energy of the event, √s, can be estimated by measuring the deflection angles of the electron and positron from the beam axis. It has been shown that the most straightforward approach is to use the particles scattered between 0.1 and 0.3 radians. At those angles, the reconstruction can be accomplished using the the forward tracking detector, which has high angular accuracy, and helped by calorimeter endcap for the lower energy events.
The reasons why this is the preferred process to estimate √s are that it has better statistics than the physics channels (400 times the μμ rate in our angular range), and it has a good energy resolution. At small angles, the error on on √s grows, becoming more significant below 0.1 radians.
The process is basically described by the exchange of a virtual photon, or a Z0 boson. In our angular range, the s-channel dominates, and the Z0 contribution is small.[lep precision physics]
From outgoing particle angles the momentum loss can be estimated, and thus the energy loss from nominal energy, under the assumptions that a.) only one photon has been radiated and b.) it was radiated along the beam.
The distribution of √s will then give the luminosity spectrum, ∂L/∂√s.
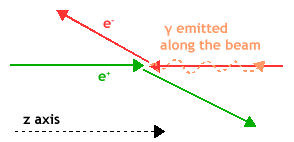
Fig f: bhabha scattering event schematic diagram
Two methods have been considered in the course of the project:
The angles θ1 and θ2 are defined as shown in fig. f. The acollinearity angle θA is equal to the difference of θ1 and θ2 ( θA = θ1 - θ2 ).
The angle θ is taken as the average between θ1 and θ2. For small acollinearity ( θA<< θ), we have θA=(Δp/pb)sinθ, where Δp = p1-p2, the momentum difference between the two particles at collision.
The quantity needed is √S ≈2pnom - θApnom/sinθ by this estimate.
Considering the error: for small θA , if the error is Gaussian, σ√s≈ σΔp ≈ σθApb/sinθ ≈ √ σpb.
So the error increases as the scattering angle θ approaches 0, which implies better luminosity resolution for slightly liarger angles.
This approximation can be derived directly from bhabha scattering kinematics (cf. Appendix B): if the 4-momenta of an electron and a positron are added to find the center of mass energy, and it is assumed that a.) one photon is radiated in the direction of the beampipe, and b.) the paths are coplanar, then some algrebra will yield:
√s ≈ √cot (θ1/2) cot (θ2 /2) cf. Appendix B for algebra.