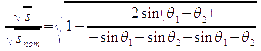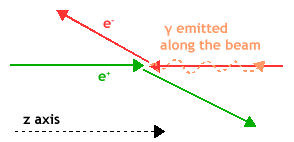
We consider the four vectors of the following interaction:
Consider the the four momenta of the electron and positron, before and after the collision.
We can solve
all the following algebraic equations using Mathematica(TM).
From momentum conservation, we should have:
(*)
where
the
and
refer
to the electron and postiron 4-momenta, and the subscrpts i and f
refer to their initial and final states.
We can also write:
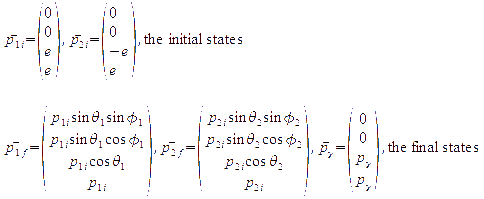
for the initial states, and the final states deflected at arbitrary angles θ and φ; the photon final momentum is in the z direction, along the axis.
Solving the vector equation (*) above, set φ1 = 0, φ2 = π (the interaction is coplanar.)
If we further set the squared center of mass energy, S = | p1 + p2 |,
and divide by the nominal energy Snom = √p1 p2
we get the result:
,
which is algebraically equivalent to the result quoted by K. Mönig
in ref [1Monig reconstruct paper]:
