It could be argued that particle physics is currently languishing in one of its least interesting periods since the inception of quantum mechanics at the turn of the 20th Century. As a discipline that thrives on the discovery of new particles to advance both the theoretical and conceptual understanding of its many intricacies and complexities, not since the discovery of the bottom quark in 1977 [1] has particle physics been pushed forward by the appearance of an unexpected new particle1. Although the recent progress made in the measurement of neutrino oscillations points strongly towards physics beyond the Standard Model, very little experimental evidence exists that can be used to guide the creation of theories that properly describe this physics. The many varied theories that exist under the banners of the Higgs Sector, Supersymmetry or “Grand Unified Theories” (GUT's) predict an enormous cornucopia of particles that could exist at energies that have yet to be reached by modern particle accelerators.
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
The current Standard Model of particle physics is an impressively robust theory. A result of almost a century's observation and refinement, it encompasses virtually every observation that has been made in the field of particle physics. The myriad of bound states, decay products and interaction cross sections are all accounted for within the Standard Model: the resulting particle coupling and decay calculations based upon the Standard Model are some of the most accurate known to man. In the Standard Model, all matter is made from two types of elementary particle: quarks and leptons. The interactions between these fundamental particles are mediated by a third group of particles — the mediators — which are themselves subdivided by force: the photon (γ) for the electromagnetic force, the W+, the W− and the Z0 for the weak force and eight gluons (g) for the strong force2. All the fundamental particles of the Standard Model are summarised in Table 1.1 [2].
The basis of the Standard Model is the underlying symmetry group SU(3)c×SU(2)L×U(1)Y: the SU(3) group describes the strong force while the electromagnetic and weak forces are unified into a single force under the SU(2)×U(1) group [3]. The unification of the electroweak sector, by Glashow, Weinberg and Salam (the GWS model) provided an explanation for the charged weak interactions, via W± exchange, and successfully predicted their masses, along with the existence and mass of the Z0. However, in unifying the weak and electromagnetic forces, it is no longer possible to maintain the exact symmetry of SU(2)×U(1): nature spontaneously breaks this symmetry and the W± and Z0 gain a mass, while the photon remains massless. To account for this electroweak symmetry breaking, something extra must be introduced: the Higgs boson.
To account for the spontaneous symmetry breaking in the electroweak sector, a Higgs field is introduced into the Standard Model Lagrangian [4]. The ‘residue’ of this Higgs field, according to the basic Higgs theory, is a single scalar boson, known as the Higgs boson. It is the manifestation of this Higgs field, and the consequent appearance of the Higgs boson, that is predicted to be the cause of electroweak symmetry breaking [4]. The resultant hypothesis is therefore that the Higgs field is the cause of all the fundamental particle masses and that the Higgs couples to all massive particles, with a coupling strength that is dependent upon the particle's rest mass [1].
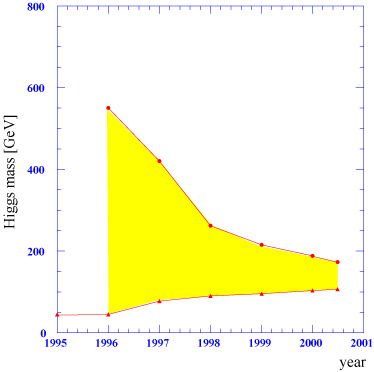
| Figure 1.1: The narrowing of the allowed mass range for the Standard Model Higgs boson as a result of precision electroweak measurements at LEP, SLD and the Tevatron (the yellow region shows the upper and lower 95% confidence limits) [5]. |
The Higgs has so far escaped detection, although this is not for lack of trying: data from the last run of the Large Electron Positron collider (LEP) at CERN gave a possible indication of a Higgs with a mass around 114 GeV [5]. However, while the Higgs has not yet been found, measurements with current accelerators do give an indication as to the most likely mass range of the Standard Model Higgs: this is shown in Fig. 1.1. If and when the Higgs is finally found, the probing of the properties of this elusive particle will be essential in the creation of theories that lie beyond the Standard Model. Part of this reshaping of the current landscape of particle physics requires the investigation of physics at the current high energy frontier: it is at these TeV energies that vital experimental evidence for physics beyond the Standard Model will be most forthcoming.
Theories abound as to what lies beyond the predictions of the Standard Model and the Higgs sector. However the candidate that is currently favoured is the concept of Supersymmetry (SUSY). Supersymmetry is based on the idea that every fundamental fermion has a bosonic “superpartner” and vice versa [4]. The superparticles (or ‘sparticles’) have properties that would ideally differ from their Standard Model partners only for the particle's spin. However, this symmetry is clearly inexact, since none of the particles predicted by supersymmetry have been seen. The cause of this discrepancy is similar to electroweak symmetry breaking: the particles and sparticles begin with identical masses and nature spontaneously breaks the symmetry between the two. This results in the sparticles having much larger masses — a necessary condition since none have yet been found. SUSY therefore makes a number of distinct, testable predictions as to the existence of particles outside the Standard Model: in addition to the large number of sparticles, SUSY theories propose the existence of a number of Higgs particles (2 charged and 3 neutral) [6]. The predictions of the cornucopia of supersymmetric theories have yet to be confirmed, but are likely to come under a great deal of scrutiny with the next generation of particle colliders (see Section 1.2)3.
Extensions to this Minimal Supersymmetric Standard Model (MSSM) are varied and provide a number of benefits over the Standard Model. One possibility is the unification of gravity into the forces currently covered by the Standard Model into a Grand Unified Theory (‘GUT’): these place all the forces of nature onto an equal footing, unifying the coupling strengths at a very high energy scale (the so called ‘GUT scale’) [5]. In addition, the various string theories make predictions about the existence of extra dimensions in addition to the appearance of supersymmetry. These theories however will have to wait until more light is shed on physics beyond the Standard Model.
Neutrino oscillations also point the way to new physics. However they are not, of themselves, indicative of physics that truly lies outside the scope of the Standard Model, since it is possible to incorporate these effects into the Standard Model without a great deal of adjustment4. To discover physics that lies beyond the Standard Model, it is essential that particle physics steps beyond the reach of its current tools (the high energy colliders) to attain energies that mean that particle physics can step forward once again into the unknown.
There are a number of ways to investigate the physics that exists outside that encompassed by the Standard Model. It is possible to make precision measurements on some of the predictions of the Higgs sector and non-Standard Model physics with existing accelerator facilities [3]. However, to have direct access to this new physics, new accelerators are required that are capable of reaching these TeV-scale energies. Traditionally (and somewhat erroneously) hadronic machines have been thought of as ‘discovery’ machines, with lepton colliders used as complementary ‘measurement’ machines; the reasons for making such a distinction are given in the next section. However, the choice of beam itself constrains the design of the accelerator: this choice of accelerator design is discussed in the remainder of this chapter.
It is highly likely that the first evidence for any such new physics will be found at either the Tevatron at Fermilab, or almost certainly at the Large Hadron Collider (LHC) at CERN5 [7]. However, neither of these machines will provide the required precision measurements that are needed to test the many postulated extensions to the Standard Model [6]. This is because, unlike LEP — which (as its name would suggest) was designed to collide electrons and positrons — both these accelerators are hadronic: the LHC will use two 7 TeV proton beams, with the Tevatron using 1 TeV proton-antiproton collisions [8]. While these energies are easier to achieve with hadron accelerators (see Section 1.2.2) — making new, high energy discoveries easier as a result — the methods of Higgs production at leptonic and hadronic machines are broadly similar, they are invariably simpler for e+e− collisions [5]. In addition, two features lend themselves extremely favourably to lepton collisions: one is the cleanliness of the interaction and corresponding final state, and the other is the precise initial state energy.
The cleanliness of the lepton interaction is primarily a result of its simplicity, since electrons and positrons are both fundamental point-like particles. In an interaction between the two, there is no “excess baggage”: the collision results in the complete annihilation of both particles and a resultant state with all of the energy of the two colliding leptons and zero net charge. However, in hadronic collisions the interaction occurs between quarks within the composite structure of the hadron, usually via some gluon or W± exchange. Therefore the interaction is both impossible to define prior to the collision and extremely messy: the nature of quark and gluon jets, resulting from the confinement of strongly interacting particles, leads to an enormous number of final state particles compared to lepton collisions, with a good deal more work required to reconstruct the primary vertices of the event.
In addition to the complexity of the interaction, the composite nature of hadrons means that there is no way of precisely defining the energy of each quark prior to collision: only a portion of the total energy of the proton is carried by each quark, so that the resulting interaction does not have a definite initial energy. This is not the case for leptons, since each one carries exactly the same, well-defined energy into the collision. It is therefore possible, with a lepton collider, to precisely vary the energies of the incoming particles and scan the available energy range to measure the energy dependence of particular production cross sections.
A further benefit of e+e− colliders, is the ability to precisely define the helicity of the initial state particles6 and measure the spin dependence of various final states, something that is not possible for hadronic interactions. For these reasons, precision tests of the properties of the Higgs — such as the mass, width, production cross sections, branching ratios and self-coupling — and of the myriad of supersymmetric particles (primarily the light supersymmetric particle, or LSP) are possible only with a lepton collider [9].
There are suggestions that a muon collider, using μ+μ− rather than e+e− beams, would provide the necessary clean interactions while making use of a modified synchrotron design (for more details, see [10]). However, the problems associated with using stable muon beams, primarily related to their short lifetime and consequent beam damping requirements, mean that a muon collider is not currently a feasible prospect. It is therefore necessary to resort to the well-understood tactic of using e+e− collisions, for which a linear collider is required.
The method of charged particle acceleration employed for the two main accelerator designs — the linear accelerator and the synchrotron, or circular accelerator — is essentially identical: this involves the use of accelerating cavities to produce a high voltage gradient through which the particles are accelerated, and is described in detail in Chapter 2. However, there are a number of fundamental differences between the two accelerator types, both of which have their relative merits.
| Figure 1.2: The overall view of the 27 km CERN Large Hadron Collider (LHC), showing the location of the four main experiments: ATLAS, CMS, LHCb and ALICE [11]. |
The synchrotron uses a series of accelerating cavities, arranged in a circle and interspersed with dipole magnets that bend the beam and cause it to travel continuously through a circular orbit [12]. As the accelerated particles become more energetic and their velocity increases, a higher magnetic field is required to bend the particles through the same trajectory. As such, the strength of the bending magnets is adjusted accordingly, to keep the particles on the same orbit. The accelerating field within the cavities is also adjusted so that, as the particles pass more frequently through each cavity, the maximum acceleration is still imparted to the beam; for ultra-relativistic particles the velocity is approximately constant, at the speed of light c, and the RF frequency remains constant. The accelerator currently under construction at CERN is the 27 km LHC which makes use of the circular LEP tunnel, and is shown in Fig. 1.2.
The advantage of using the synchrotron principle is that the same accelerating cavity can be used many times to continuously accelerate the beam, resulting in a certain economy of components. A collider based on the synchrotron design, such as the LHC, will accelerate two beams in opposite directions around the circular trajectory many times, on each occasion increasing the energy of the beam. The beams are then brought into collision at various Interaction Points (IP's) around the circumference of the accelerator: the four experiments at the four IP's of the LHC can be seen in Fig. 1.2. When two beams are brought into collision, the vast majority of particles do not interact at all, but pass through the IP without hindrance. As such, the beam is re-accelerated and re-used many times, before the cumulative effects of the continuous collisions force it to be discarded and the process begun afresh.
| Figure 1.3: An overhead schematic of the Next Linear Collider [13]. The full length of the accelerator at 30 km is larger than the circumference of the LHC. |
The linear accelerator, or linac, is more primitive in concept. The beam is accelerated along a single straight trajectory, from which the accelerator derives its name. The energy of the beam is therefore proportional, for a given accelerating gradient, to the length of the accelerator, since the beam passes only once through each accelerating cavity. Two accelerator paths are required — one for each beam — and the two meet at a single IP7. After passing through the IP, the beam is then discarded into a beam dump, with a new bunch used for each collision. A schematic diagram of the layout of the Next Linear Collider (NLC) — one of the planned next generation linear colliders — is shown in Fig. 1.3.
Although the linear collider seems, at first glance, extremely wasteful in comparison to the synchrotron, there are a number of circumstances in which the performance of the linear accelerator is superior. These relate to a number of shortcomings of the synchrotron: the foremost amongst these is the production of synchrotron radiation. Synchrotron radiation is the emission of EM radiation by any relativistic charged particle that undergoes an acceleration [14]. When the acceleration is in the direction of the particle's motion — such as in an accelerating cavity — the synchrotron radiation emission is negligible. However, when the acceleration is perpendicular to the particle trajectory — such as is applied by the field within the bending magnet of a synchrotron — the energy loss by synchrotron radiation is a significant fraction of the particle energy. This radiation is emitted in a narrow cone that is approximately collinear with the direction of travel of the particle. In addition, the energy loss for a particle deflected through a particular angle scales with the beam energy as E4, strongly influencing the size of the synchrotron required to reach a particular beam energy.
The radiated power due to synchrotron radiation also depends on the rest mass of the radiating particles like 1/m4 [15]. This is the primary reason behind replacing the LEP electron-positron collider with the proton-based LHC, since the energy loss for protons within the same ring is a factor of 1013 smaller than that for electrons at the same energy8. As such, the LEP accelerator — with a beam energy of around 100 GeV within a 27 km ring — represents something of an upper limit in terms of an electron-positron collider that utilises the synchrotron design. As physicists attempt to push to higher energies, it becomes increasingly difficult to replace the enormous power dissipation through synchrotron radiation. A linear collider, however, suffers from no such shortcomings. The beam energy is independent of the particle mass and is dependent only on the number of accelerating cavities (i.e. the length of the accelerator) and the gradient of each cavity.
Another problem with the synchrotron stems from the number of collisions that each bunch has to undergo. The primary goal of any collider is to maximise the Luminosity L. The luminosity is a measure of the number of interactions that occur between particles in the two colliding bunches (and is usually given in units of cm−2s−1) and is defined as:
|
for number of particles per bunch N, number of bunches per train n and machine repetition rate f; HD is the beam pinch enhancement, resulting from the interaction of two oppositely charged bunches (see Section 2.4.3); σx* and σy* are the horizontal and vertical (r.m.s.) beam dimensions at the IP [16]. Clearly, since the luminosity increases for more densely-packed bunches (i.e. smaller beam spot size) and a higher interaction rate (i.e. increasing the frequency of bunch crossings at the IP), the luminosity is maximised by minimising the cross-sectional area of the beam and maximising the frequency with which the bunches are brought into collision. While both types of accelerator can take advantage of more frequent bunch crossings9, a linear collider is able to make use of a much smaller spot size, due to the nature of the beam-beam interaction (see Section 2.4).
Although only a small fraction of the particles within the two colliding bunches actually annihilate to produce new particles, the rest of the bunch does not pass through unaffected. The large EM-fields produced by each bunch, as a result of the large number of charged particles moving at near-light velocities, produce a large force on the opposite bunch. Since a linear collider throws away its bunches post collision, any detrimental effect that the process of collision has on either bunch is irrelevant. A synchrotron, however, must do its utmost to maintain the integrity of each bunch, since each one is recycled and used for multiple collisions. This means that, by squeezing the bunches into a very flat geometry with virtually zero cross-sectional area (and hence increasing the destructive nature of the beam-beam interaction), the linear collider carries a distinct advantage (the full reasons for the selection of such a geometry are given in Section 2.4).
For these reasons it is necessary to construct a linear collider to fully probe the physics that lies outside the reach of the current technology, beyond the Standard Model. A number of technical challenges exist, mainly in the areas of high gradient accelerating cavities and power delivery systems, that must be overcome in order to construct a linear collider capable of delivering the 500 GeV and above collisions required to probe into this new physics. These are described, along with the generic design of the linear collider, in the next chapter.
1 Although the top quark was discovered after the bottom, it was one of the most widely predicted particles ever to be discovered. In fact, one could say that the last truly unexpected new particle to be discovered was the charm quark, since the discovery of the
2 Gravity has proved to be the one stumbling block that the Standard Model has been unable to account for. It is one of the aims of “Quantum Gravity” theories to be able to unify the Standard Model forces with General Relativity to place all the known forces of nature on an equal footing. The preliminary suggestion is that gravity is mediated by a spin-2 boson called the graviton.
3 It has been said that “The predictions of the Higgs sector and supersymmetry are likely to be completely wrong, but are our only useful reference point.” [3]
4 Neutrino oscillations arise from a mixing of the mass eigenstates with respect to the weak neutrino eigenstates: this essentially means that, while retaining their weak eigenstate, neutrinos can oscillate between the mass eigenstates. This is similar to the mixing of quarks that results in flavour-changing quark decays, mediated by the W±, and is only possible if the neutrinos have mass.
5 Conseil Européen pour la Recherche Nucléaire, or European Organisation for Nuclear Research.
6 It is theoretically possible to set the initial spin states of both leptons in an e+e− collision: experimentally, certain difficulties must be overcome, such as the production of spin-polarised positrons, that reduce the net spin polarisation of the two beams to less than 100%.
7 The current design for the NLC includes an option for two IP's — one high and one low energy (see Fig. 1.3) — but the two cannot be operated concurrently, since each bunch can only be used once.
8 The energy loss from synchrotron radiation is actually dependent on γ4, where
9 This process is more economical for circular accelerators, since each bunch can be recycled rather than being accelerated from scratch.
© Simon Jolly 2003