Update on Toy Fitting for the Quasi-Elastic Axial Vector Mass
Introduction and Methodology
- Basics:
- I am attempting to apply a K2K-style analysis to the Q^2 distribution of a QEL-like sample.
- Different values of the quasi-elastic axial vector mass (M_A^QEL) will change both the normalisation
and the shape of the Q^2 distribution for QEL events.
- Idea here is to use 2 sets of MC. The first set is reweighted to a number of different values
of M_A^QEL and the second 'mock data' set is also weighted to an obscure value of M_A^QEL.
- The mock data QEL-like sample Q^2 distribution is compared with a basic histogram chi-squared
test statistic to the QEL-like sample Q^2 distributions of each of the weighted MCs.
- This procedure maps out the M_A^QEL v.s. chi-squared plane and the resulting histogram is fitted
with a quadratic. The minimum gives the best fit M_A^QEL and a search for delta(chi-squared)
equal to one (as this is a 1D fit) gives the 68% confidence limits on the best fit value.
- More details:
- All MC used is cedar-carrot and has the relevant energy corrections. The MC is not weighted
with SKZP but just with the MODBYRS3 generator weights and the appropraite weighting of
M_A^QEL.
- The weighted MC samples and the mock data sample all correspond to ~5e18 POTs. Bear in mind that
this is 1/20th to 1/30th of the available real data.
- All events undergo my QEL analysis pre-selection cuts (Pitt. fiducial volume, only 1 track etc...)
and a CC-like sample is selected with the usual cut on the standard cedar-carrot CC PID.
- A QEL event selection is then applied to this CC-like sample.
- The chi-squared is defined as the sum over bins of (data bin content - MC bin content)^2/(data bin content)
- Fit options:
- The QEL-like sample selection can be chosen from the following methods that span the sensible range
of sample efficiencies and purities:
- Zero hadronic energy: ~25% efficiency and ~76% purity
- Hadronic energy less than 250 MeV: ~49% efficiency and ~62% purity
- Invariant mass less than 1.3 GeV: ~82% efficiency and ~47% purity
- The range in Q^2 over which the fit is performed can be set.
- The binning of the fitted Q^2 distribution can be varied.
- The slice in reconstructed neutrino energy from which the Q^2 distribution is taken can be varied.
- The fit can be selected to be 'shape only' or 'shape and normalisation'. When I say shape only I mean
that the distributions are normalised to area and when I say shape and normalisation I mean that the
samples are normalised to POT.
- A weighting function can be applied as a function of reconstructed neutrino energy to simulate
flux/cross section changes.
Example Fit to Illustrate Method
- Fit option settings:
- Invariant mass less than 1.3 GeV selection
- Fitting for 0.0 < Q^2 < 1.0 in bins of width (1000/9) MeV^2
- Fitting for 0.0 < Reco. Enu < 120.0 GeV
- Performing shape and normalisation fit
- Mock data weighted to 1.145 * nominal M_A^QEL
Figure 1a. Reconstructed Q^2 for QEL-like Samples
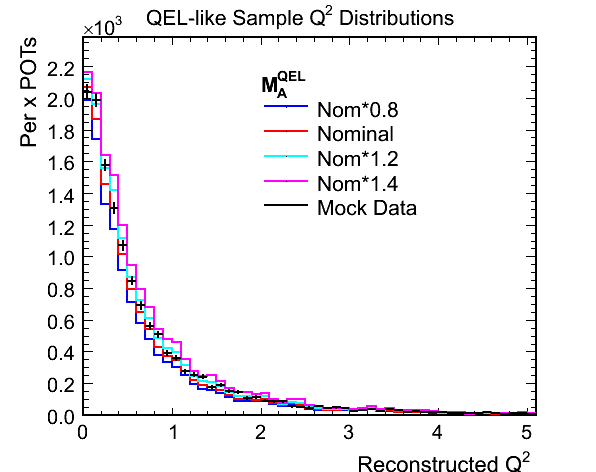
Figure 1b. Reconstructed Q^2 for QEL-like Samples Used in Fit
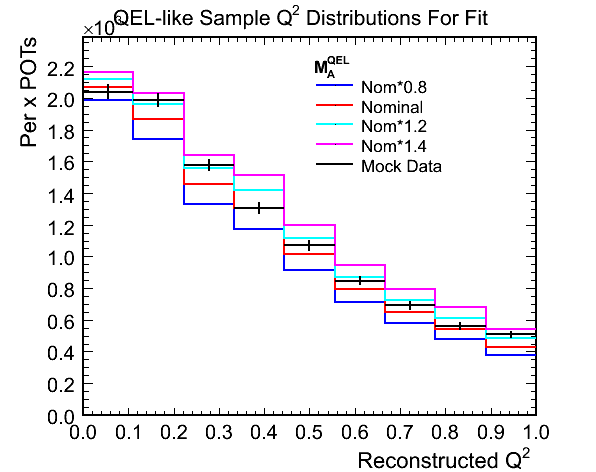
Figure 1c. Ratios of Mock Data / MC for Above
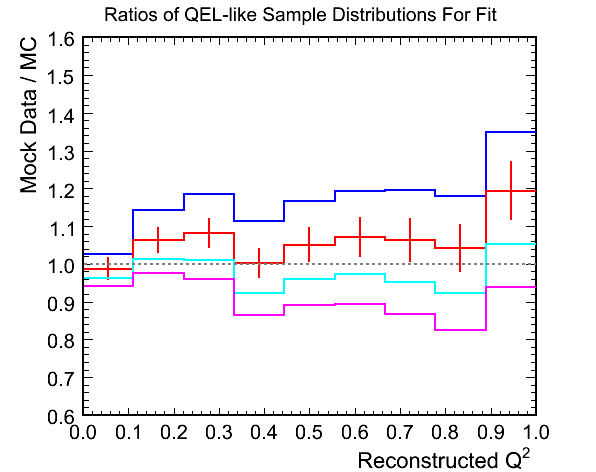
Figure 1d. M_A^QEL v.s. Chi-Squared per Ndf Fit
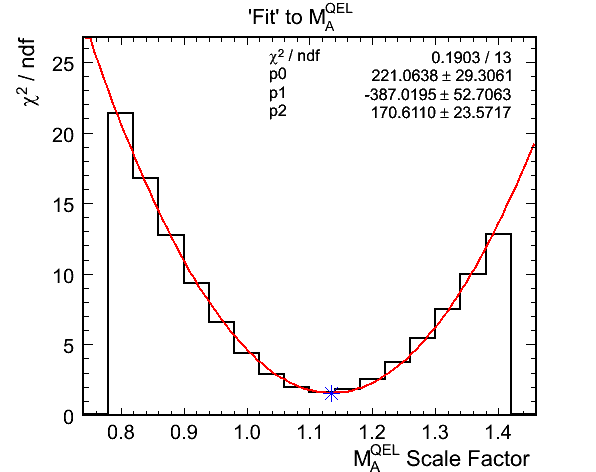
- Fit results:
- True mock data M_A^QEL scale: 1.145
- Best Fit M_A^QEL scale: 1.1342 +- 0.0255
- Chi-squared at best fit: 14.2375 (1.5819 per DoF)
- Comments:
- The true M_A^QEL scale factor is well inside the 68% confidence limits on the best fit value. Later I will show how
the fit options affect the returned best fit value and errors.
- The ratio plot illustrates why the method works. There is a shape difference in the Q^2 distribution, most visible
at the peak, that shows up as a slope in the ratio plot and a normalisation difference between the various weighted
MCs. The difference between the tails of the Q^2 distributions can only really be interpreted as a normalisation
with the statistics of the above plots.
- Later I will show the same ratio plots for the higher purity QEL-like selection methods and they will exhibit larger
differences in shape and normalisation due to their higher fractional true-QEL content. The trade off for these
purer samples is that statistics are lower in general and more specifically these selections tend to remove the
higher Q^2 events (>500 MeV^2). Maybe something like Aaron's studies into selecting higher Q^2 QEL events could
help to get a high purity sample that has reasonable statistics in the higher Q^2 region.
Fits with Different QEL-like Sample Selections
- Fit options common to all 3 selection methods:
- Fitting for 0.0 < Q^2 < 1.0 in bins of width (1000/9) MeV^2
- Fitting for 0.0 < Reco. Enu < 120.0 GeV
- Performing shape and normalisation fit
- Fit results for invariant mass less than 1.3 GeV selection (as above):
- True mock data M_A^QEL scale: 1.145
- Best Fit M_A^QEL scale: 1.1342 +- 0.0255
- Chi-squared at best fit: 14.2375 (1.5819 per DoF)
- Fit results for hadronic energy less than 250 MeV selection:
- Fit results for zero hadronic energy selection:
Figure 2. Fit Results with Different QEL-like Sample Selections (Dotted line shows true scale factor)
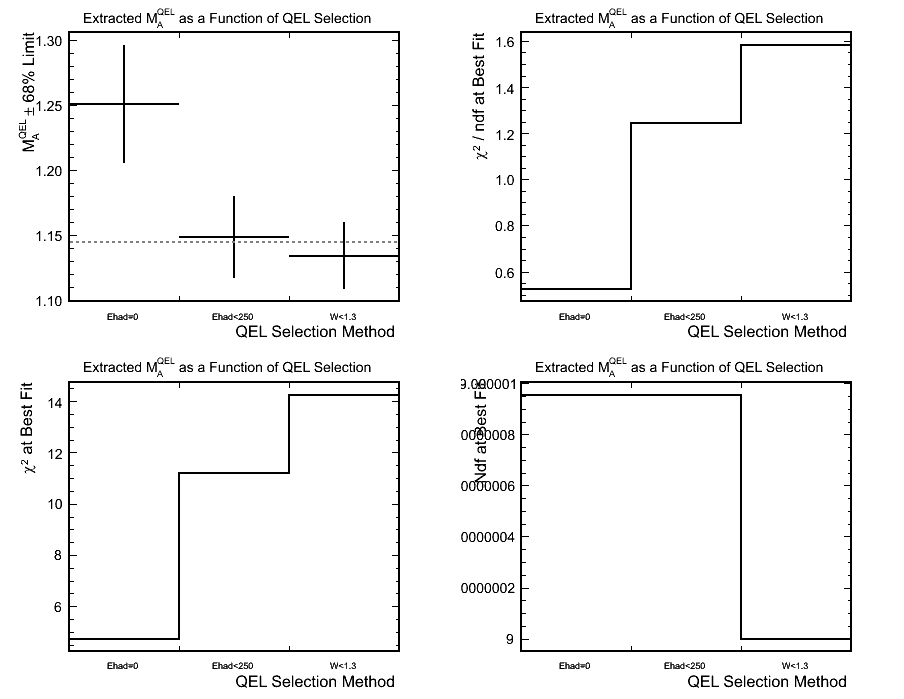
- Comments:
- Both the lesser purity sample fits get the correct result within their condifence limits but the zero hadronic energy
selection is way off, why?
- The zero hadronic energy selection has much worse statistics, less than half the events that pass even the hadronic
energy less than 250 MeV selection.
- The fit range and binning in Q^2 may be inappropriate for this method as in the tail the error bars can cover the
weighted MCs ~20% (in M_A^QEL) either side of the mock data.
- This does just seem to be a statistical problem which would not be so prevalent with the real data set. In fact
this method does look from the ratio plot to have the best separating power between the various weighted MCs (as
we would expect given the larger QEL purity).
- I should make clear that at the moment I am considering no systematic effects. Given the errors on the above fits (that
come from the statistics of the samples involved) the systematic errors will definitely dominate our ability to perform
a measurement of this kind.
Shape Only Fits
- The following plot shows the QEL-like sample Q^2 distributions for the hadronic energy less than 250 MeV selection
using area normalisation (with just the bin contents in this Q^2 range):
Figure 3. Reconstructed Q^2 for Use in Shape Only Fit
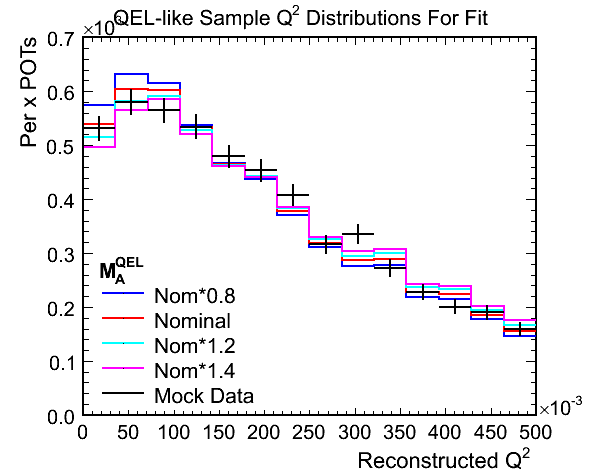
- Comments:
- Should I really perform the area normalisation over the whole Q^2 range rather than just using the bins
displayed above?
- If the sample statistics were good a shape only fit in the low Q^2 region (<500 MeV^2) could have a lot of
power in the first few bins (<100 MeV^2).
- To a lesser extent the 'tail' out to 500 MeV^2 exhibits some difference between the weighted MCs with higher
values of M_A^QEL giving a less steep falling edge to the distribution.
- The following shows an example shape only fit with options:
- Hadronic energy less than 250 MeV selection
- Fitting for 0.0 < Q^2 < 0.5 in bins of width (500/7) MeV^2
- Fitting for 0.0 < Reco. Enu < 120.0 GeV
- Performing shape only fit
Figure 4a. Reconstructed Q^2 for QEL-like Samples
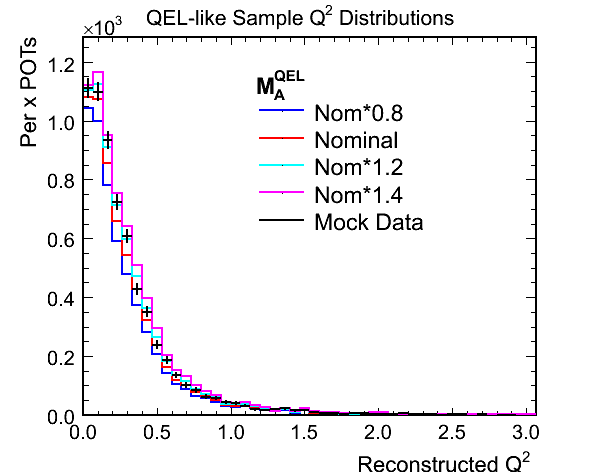
Figure 4b. Reconstructed Q^2 for QEL-like Samples Used in Fit
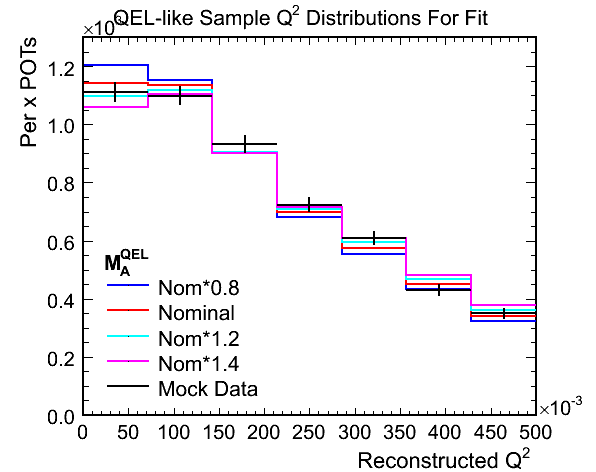
Figure 4c. Ratios of Mock Data / MC for Above
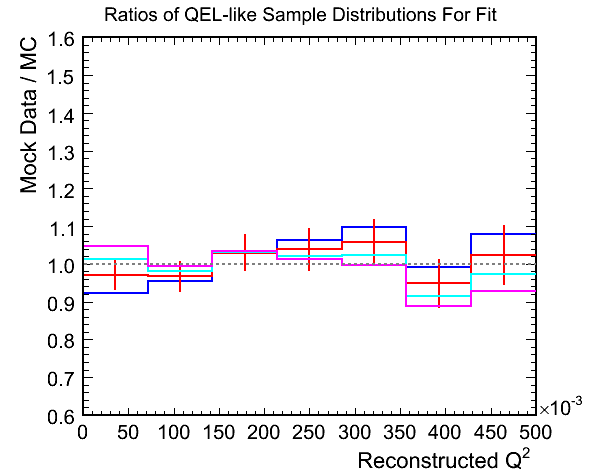
Figure 4d. M_A^QEL v.s. Chi-Squared per Ndf Fit
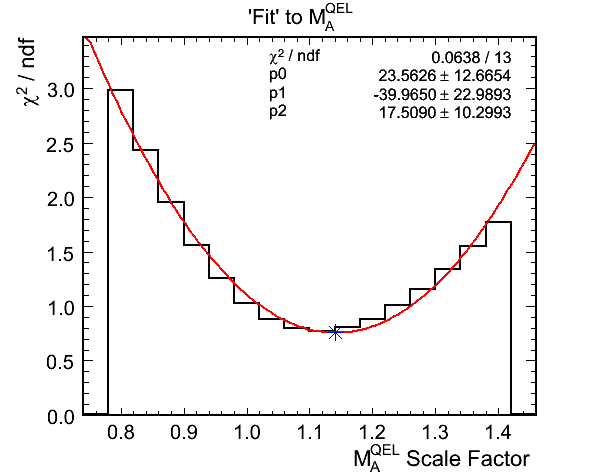
- Fit results:
- True mock data M_A^QEL scale: 1.145
- Best Fit M_A^QEL scale: 1.1413 +- 0.0902
- Chi-squared at best fit: 5.3001 (0.7572 per DoF)
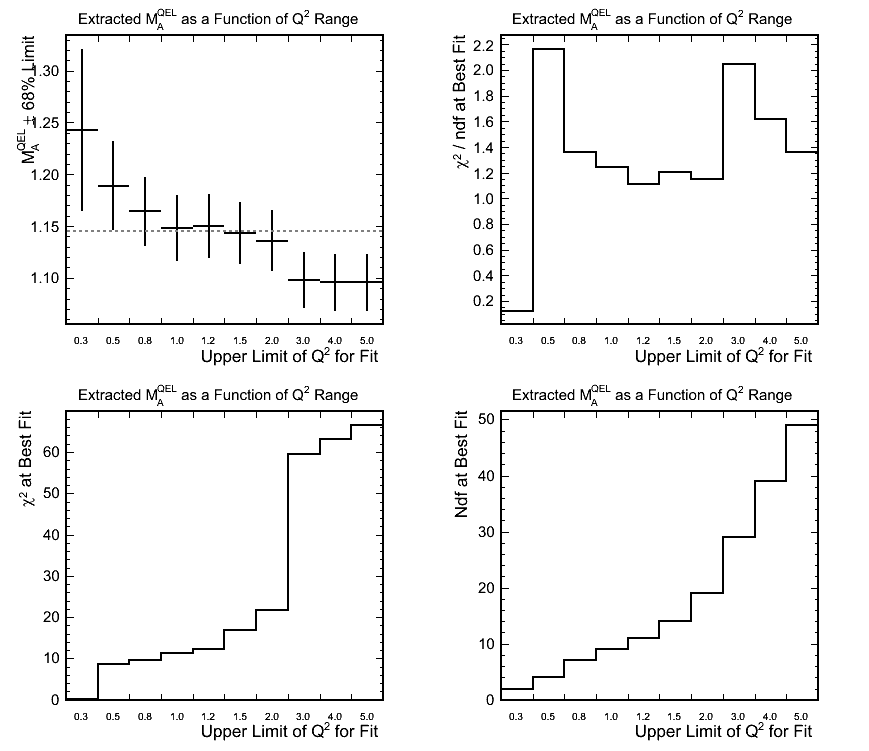
Effect of Q^2 Range Used for Fitting
Figure 5.
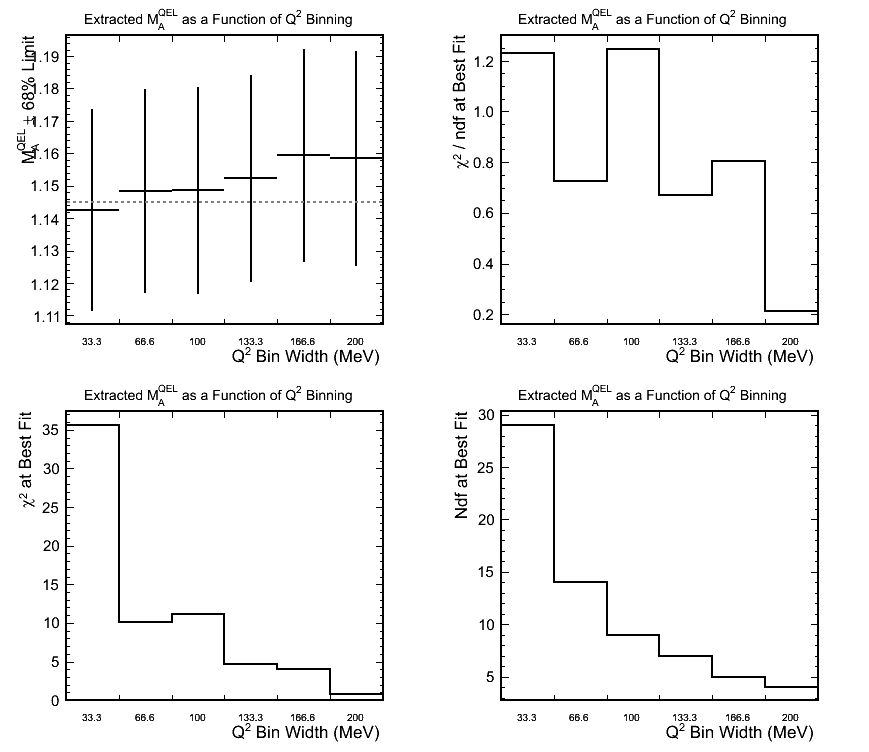
Effect of Q^2 Binning Used for Fitting
Figure 6.
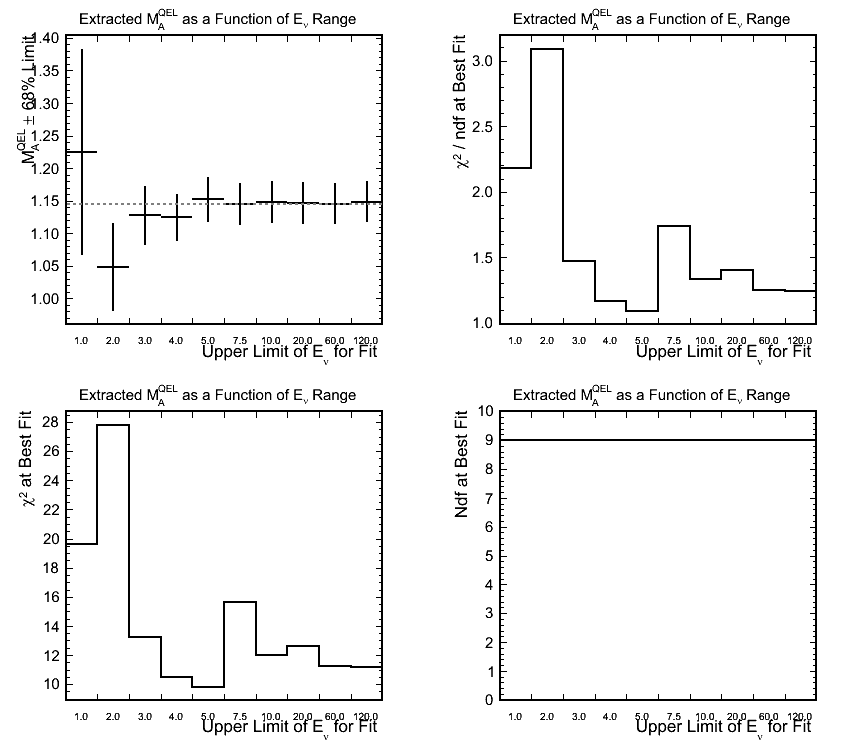
Effect of Reconstructed Neutrino Energy Range Used for Fitting
Figure 7.
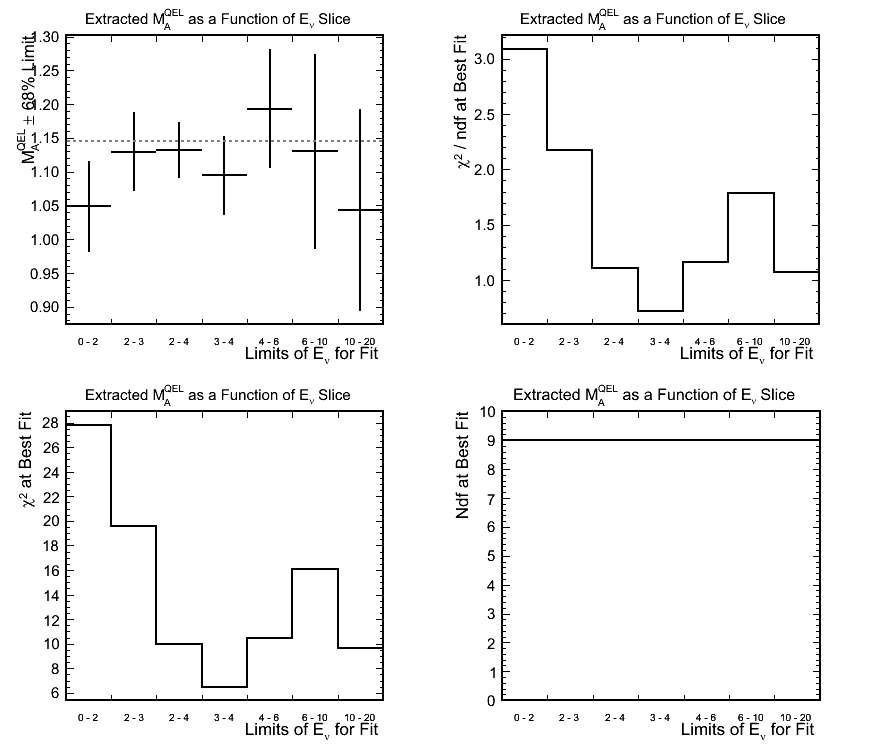
Effect of Reconstructed Neutrino Energy Slice Used for Fitting
Figure 8.
Effect of Adding 'Systematic' Effects to Mock Data
- In this section I will consider tweaking the mock data and looking to see if the fit accomodates this change in the
expected way as an effective change in M_{A}^{QEL}.
- I will start by considering an event weighting that is applied as a flat function of the reconstructed neutrino energy
with fit options:
- Hadronic energy less than 250 MeV selection
- Fitting for 0.0 < Q^2 < 1.0 in bins of width (1000/9) MeV^2
- Fitting for 0.0 < Reco. Enu < 120.0 GeV
- Performing shape and normalisation fit
Figure 9a. Illustration of Weighting
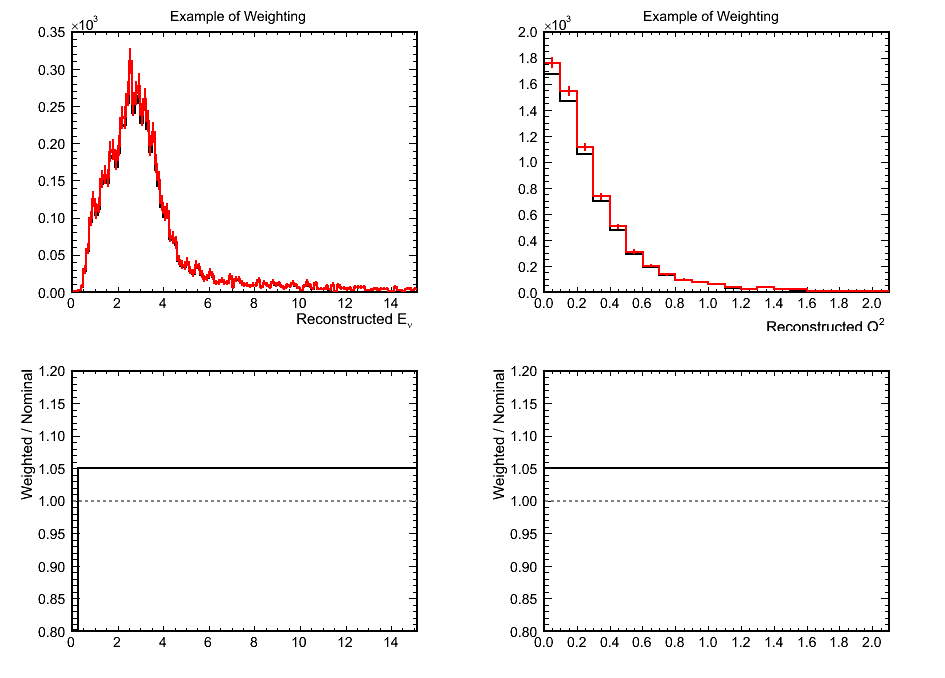
Figure 9b. Reconstructed Q^2 for QEL-like Samples Used in Fit
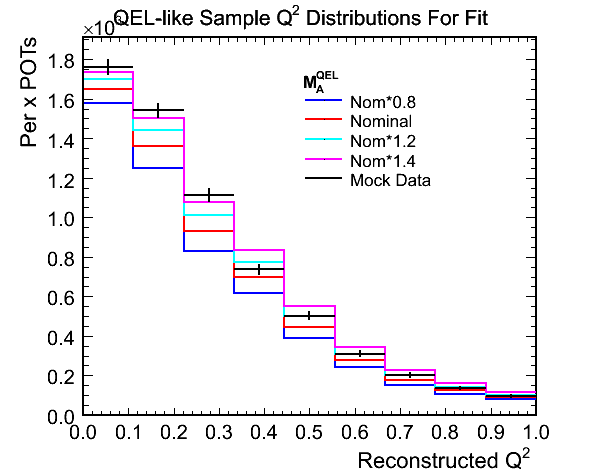
Figure 9c. Ratios of Mock Data / MC for Above
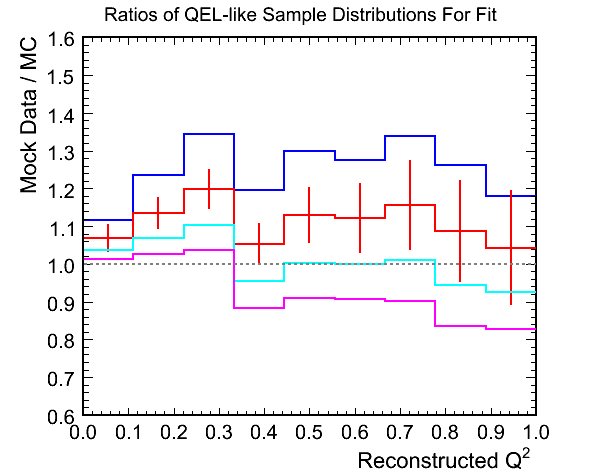
Figure 9d. M_A^QEL v.s. Chi-Squared per Ndf Fit
- Fit results for zero hadronic energy selection:
- True mock data M_A^QEL scale: 1.145
- Best Fit M_A^QEL scale: 1.2509 +- 0.0316
- Chi-squared at best fit: 17.3721 (1.9302 per DoF)
- Comments:
- The increase in weighted mock data at lower Q^2 brings it above even the highest weighted MC but the tail doesn't change
too much keeping the best fit M_{A}^{QEL} scale factor at ~1.25. This is 10% above the truth value and the mock data was
weighted by only 5%.
- In the next example I will apply weights that vary as a function of the reconstructed neutrino energy with the same fit
options as before:
Figure 10a. Illustration of Weighting
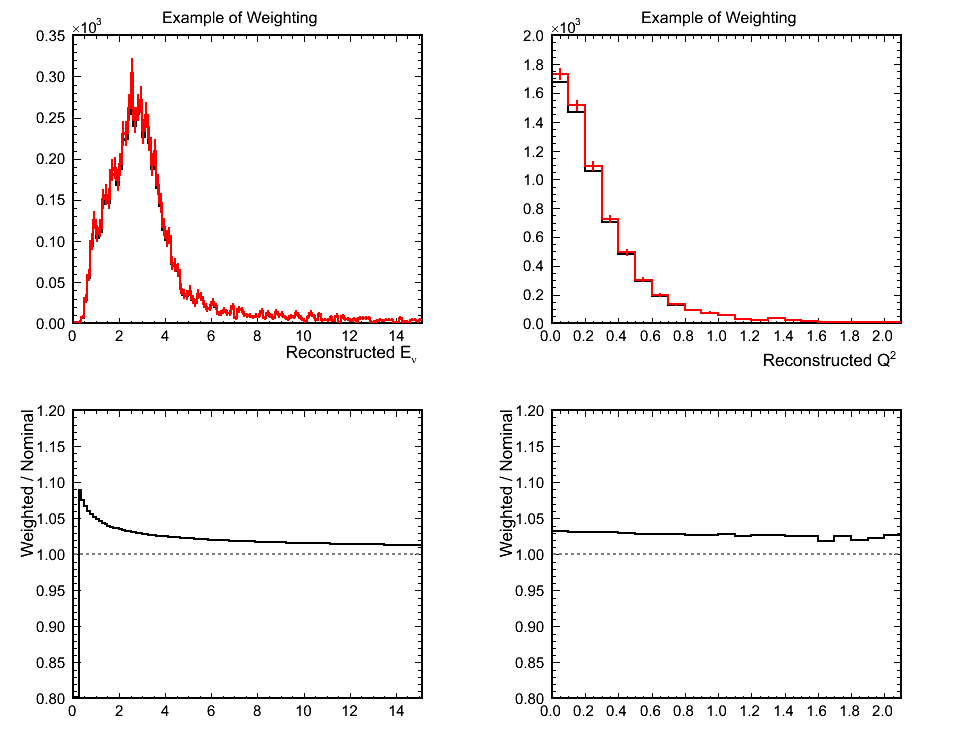
Figure 10b. Reconstructed Q^2 for QEL-like Samples Used in Fit
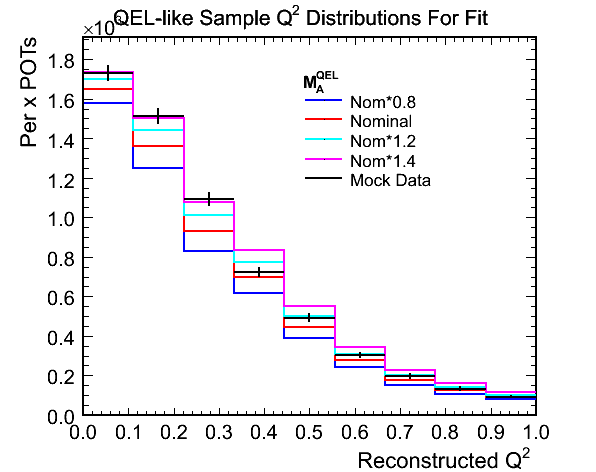
Figure 10c. Ratios of Mock Data / MC for Above
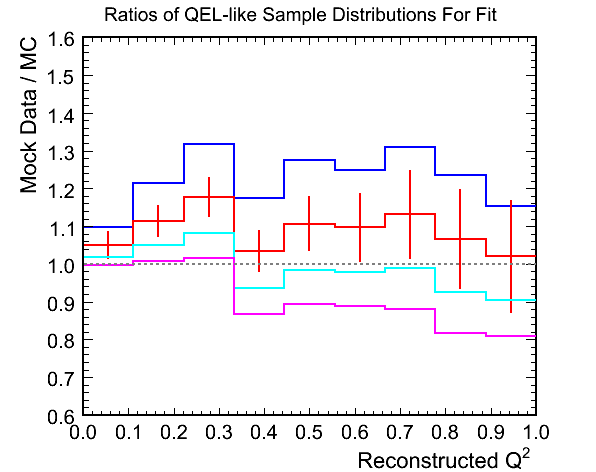
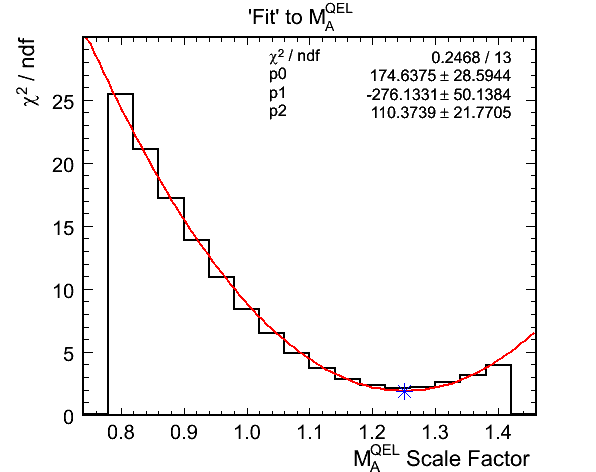
Figure 10d. M_A^QEL v.s. Chi-Squared per Ndf Fit
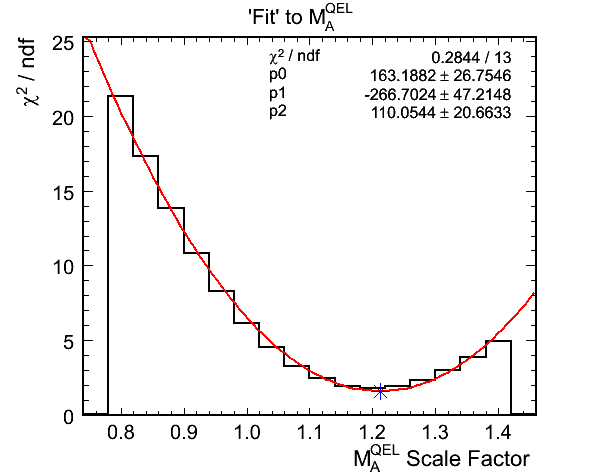
- Fit results for zero hadronic energy selection:
- True mock data M_A^QEL scale: 1.145
- Best Fit M_A^QEL scale: 1.2117 +- 0.0317
- Chi-squared at best fit: 14.4779 (1.6087 per DoF)
- Comments:
- Similar story to the first example. The best fit M_{A}^{QEL} scale factor is increased as the weighting raises up the
low Q^2 region of the QEL-like sample in the mock data.
- In this final example I will weight the mock data with the PRL SKZP beam and hadron production weights (but not the detector
weights) and re-fit the M_{A}^{QEL} scale factor. Again I will use the same fit options.
Summary, Conclusions and Further Work






















