Update on Flux Shape Work and QEL Selection

Introduction and Motivation

• One conclusion that I drew from the Fermilab collaboration meeting is that my estimated flux shape was quite sensitive to background contaminations from NC and DIS events. In particular the estimated flux shape was larger in the lower energy bins (0-3 GeV) when compared to a gnumi v17 LE-10 flux.
• There are 2 main problems here:
  • MC sample statistics - I am using the MC QEL sample to account for the RES and DIS impurities in the data sample via their Neugen cross sections and the NC impurity by directly subtracting off the expected number of NC events in a given energy bin. The statistics are small enough that fluctuations in the content of the MC QEL sample could have a big impact on the estimated flux shape.
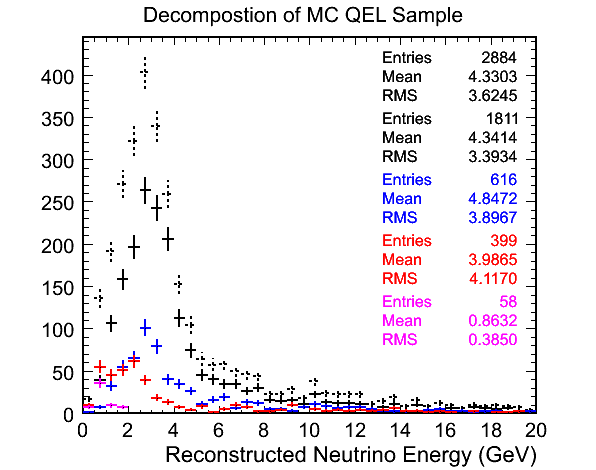
  • Sample impurity - the majority of the NC and DIS impurity is in the lower energy bins and it would be better to have as little of its possible to minimise the impact on the flux shape estimation. I am planning to investigate the characteristics of these low energy DIS and NC events:
    • True CCQE.
    • True CCDIS.
    • True CCRES.
    • True NC.

Figure 1 - Decomposition of MC QEL Sample by Process.

• One way to solve the 2nd problem and to help with the first is to increase the QEL sample purity for a given efficiency. I have started to look at some new variables to go into the ML QEL selection...

Improving the QEL Selection

• The variable that I have been concentrating is based on predicting the 4-momentum of the proton assuming that a given event is CCQE and then seeing how well the hits that I classify as part of the vertex hadronic shower agree with this.
• I define the vertex hadronic shower using the following criteria for an event:
  • remove hits that constitute part of the largest track in the event but not a shower
  • keep hits that are reconstructed as part of the track and a shower but remove ~1 MIP of their PH
  • remove any hit in the event with PH < ~150sigcors
  • remove any hit that is radially further away from the vertex than 2m - I am assuming that the protons and pions that I am interested in will not travel further than this in the detector
• I use the kinematic information in any event (muon 4-momenta, neutrino energies and neutron mass) to predict the expected proton 4-momentum assuming that the event is CCQE.
• I then construct a variable that looks at the average perpendicular distance in the (u,z) and (v,z) planes from each hit to the expected proton direction weighted by the hit PH.
• One good thing about a variable of this sort is that it should be fairly uncorrelated with the other variables I am using.

• How well am I predicting the proton 4-momenta? The following plots shows the proton 4-momentum from my prediction and the truth information from the Std Hep array for events that have 1 good track, are in the fiducial volume and have reconstructed neutrino energy less than 20GeV:
  • My predicted proton 4-momentum component.
  • That 4-momentum component from the Std Hep array.

Figure 2 - Comparison of Proton 4-Momenta.

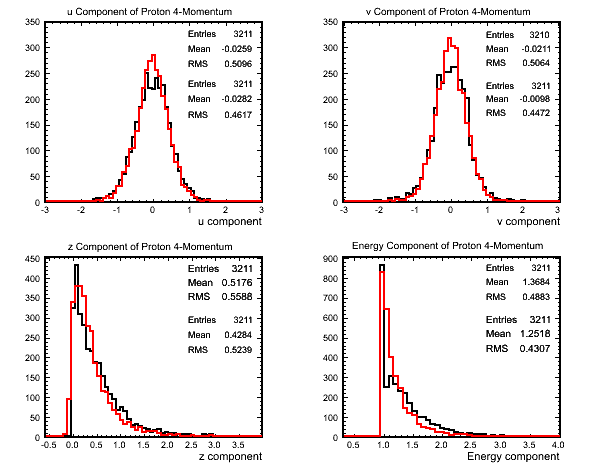
Figure 3 - Comparison of Proton 4-Momenta.

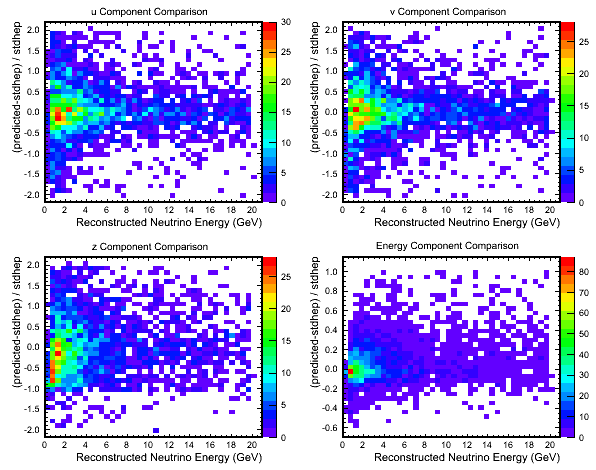
• The distributions of figure 2 look quite similar but figure 3 shows that there are quite a few events where I get the proton 4-momentum quite wrong.
• I have started to look for the cause of the disagreement in these cases...

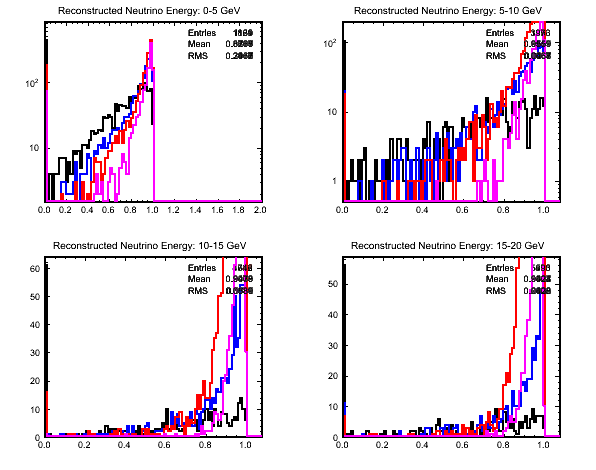
• The following plot shows the fractional error in the reconstructed muon energy for true CCQE events that have a greater than 100% error in any of the proton 4-momentum components as compared to the Std Hep array:

Figure 4 - Comparison of Muon Energies.

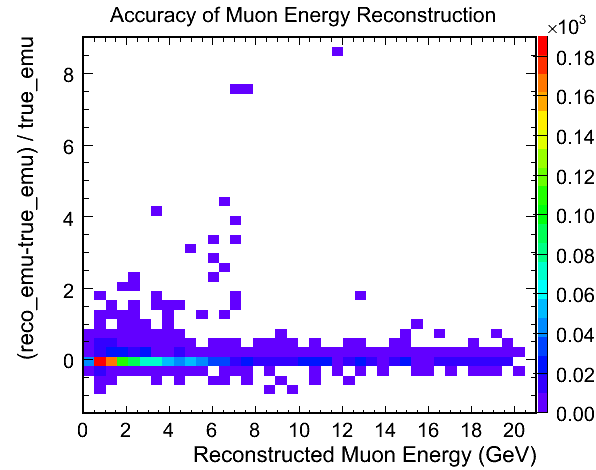
• It looks like most of the muons in the sample were reconstructed well - I need to look into the Std Hep array and perform a comparison of the reconstructed components of the muon 4-momentum with the Std Hep information about the muon to be sure.
• How much could Fermi motion be affecting the predicted proton 4-momentum accuracy?
• I also need to check that I am not doing something wrong in the code.

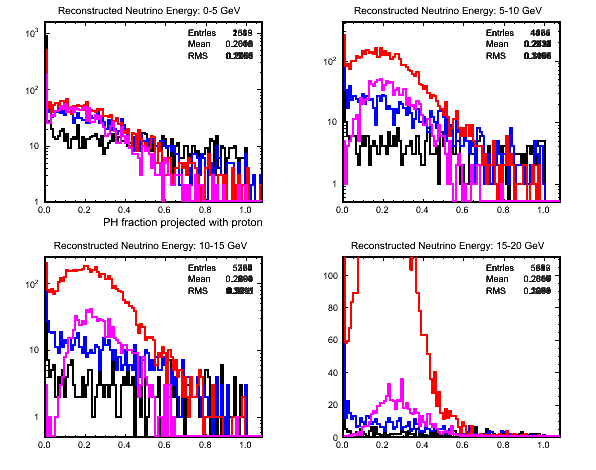
• Given the above agreement/disagreement the following figure shows the distributions of my average PH weighted perpendicular distance of a hit from the predicted proton direction variable for U planes (there is an equivalent plot for the V planes):
  • True CCQE.
  • True CCDIS.
  • True CCRES.
  • True NC.

Figure 5 - Variable Distributions by Process.

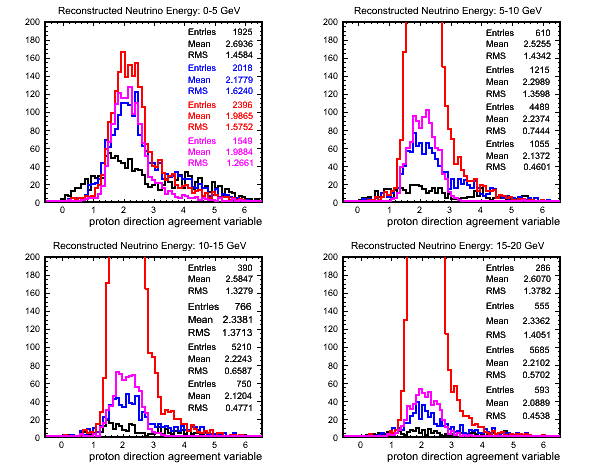
• The variable does not do so well at higher energies (although at these energies I can already to a good job) but may be useful for the lower reconstructed neutrino energy events.
• Hopefully the separation powers can be improved after I fully understand the cases where I am estimating the proton direction wrong.

Conclusions

• I am planning to verify that my code is working properly and try to encorporate some new variables into the ML QEL selection.
• Some other variables that I am considering are:
  • the sums of projections of the vertex hadronic shower hit PHs in the directions parallel and transverse to the expected proton direction as a fraction of the total vertex hadronic shower PH:
    • True CCQE.
    • True CCDIS.
    • True CCRES.
    • True NC.

    Figure 6 - VHS PH Projected Along Positive Proton Direction.

    

    Figure 7 - VHS PH Projected Transverse to Proton Direction.

    

  • coplanarity variable - for a CCQE event the muon and proton should be produced back-to-back in the (x,y)-plane and so by using the muon direction at the vertex I can define a plane for each event in which activity should be concentrated if that event is QE
• The final aim of trying different permutations of variables is to try to maximise the QE purity of my sample so as to reduce the error introduced into the estimated neutrino flux due to dealing with the background contaminations.