Project
The aim of this Master's project was to simulate the geometry and physics of a proposed Neutrinoless Double Beta Decay experiment - SuperNEMO - using a CERN simulation tool known as Geant. This was in aid of the calculation of the efficiency of the detector that can only be done by computer simulation.
From this generic setup, the following investigations were carried out:
Neutrinoless Double Beta Decay
It can be shown in Quantum Field Theories that if the neutrino is its own antiparticle ( a Majorana particle ) then a process known as neutrinoless double beta can occur. See Feynman diagram below. When no final state for a single beta decay exists, it may be possible for two neutrons to beta decay together in one process. Such a process is known as double beta decay. This is rare, being a 2nd order process, with half-lives exceeding a billion-billion years. Neutrinoless double beta decay is a variant allowed in Grand Unified Theories where the right-handed neutrino plays a role, albeit a very small one.
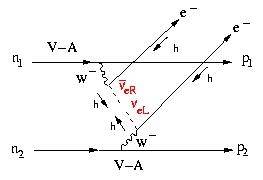In neutrinoless double beta decay, the neutrons decay into protons emitting a W- in the process as in a
single beta decay decay. And again, as usual, the W- decays into an electron and anti-neutrino. Without going into
the details, if the neutrino is Majorana in nature then it is indistinguishable from the anti-neutrino. The emitted neutrino can
then be reabsorbed by a second W- to leave only 2 protons and 2 electrons as the net result. The details lie in Supersymmetry.
Before reabsorption the anti-neutrino needs to flip to a different helicity state which is also a massive state - mass on the
order of GUTs, at least 109 GeV. Since energies available are of the order MeV, a
large energy assist is required from the
Heisenberg Uncertainty Principle. However, this means the mass helicity can only occur as a virtual particle in this decay.
NEMO and SuperNEMO
NEMO stands for Neutrino Ettore Majorana Observatory - a series of experiments looking into the phenomena of ββ2ν, and in particular striving to make an observation of ββ0ν. A collaboration, of now 50 scientists/engineers across 7 countries and 13 laboratories/institutions, since 1989, constructed two prototype detectors (NEMO and NEMO-II) which took data until 1997. The reason being that from 1994 onwards, the collaborations primary focus was upon the development of the NEMO-III detector - a large and complicated detector capable of dealing with numerous isotopes (both ββ2ν and ββ0ν candidates). NEMO-III was successfully installed in the Frejus tunnel near Modane, France and has been taking data for over a year now. As a separate project, a larger (but with simpler geometry) experiment has been proposed - SuperNEMO - which will make use of approx 100 kg of 82 Se in an ambitious attempt to detect a ββ0ν with a very minimal background count.
The HEP group at UCL joined the collaboration in 2003 and hopes that its expertise in detector design and construction will help make it and the UK major players in the development of NEMO projects and ββ0ν in general. In this section both the NEMO-III and SuperNEMO experiments will be discussed without going into the technical details. Readers are invited to visit the NEMO-III webpage or follow many links from the neutrinos site 'Neutrino Unbound'for extensive links to papers regarding the results or engineering.
The NEMO-III experiment consists of a cylinder divided into numerous detector segments (left). These distinct segments are the
feature that allows for concurrent use of different isotopes.
The double beta decay emitters (constructed from metal films or powders) are then glued to mylar strips and hung within a
segment between two concentric cylindrical tracking volumes. These tracking volumes are themselves made from approximately
6000 octagonal drift cells (track the events). Calorimeters made from a plastic scintillator, themselves connected to photo-multiplier tubes,
cover the external walls of the tracking volumes. These photo-multiplier tubes are responsible for the detection of events by energy deposition - in
NEMO-III these have a resolution of 11 - 14.5 % for a 1 MeV electron. Electrons or positrons
from pair production events are rejected by a 25 Ohm magnetic field. Outside background events such as those resulting
from cosmic or gamma rays are shielded by a layer of low activity iron surrounding the detector as well as a layer of
water. In addition, the detector is situated 1700m underground in the Frejus tunnel, a position that has an equivalent
protection of 4800m of water above it.
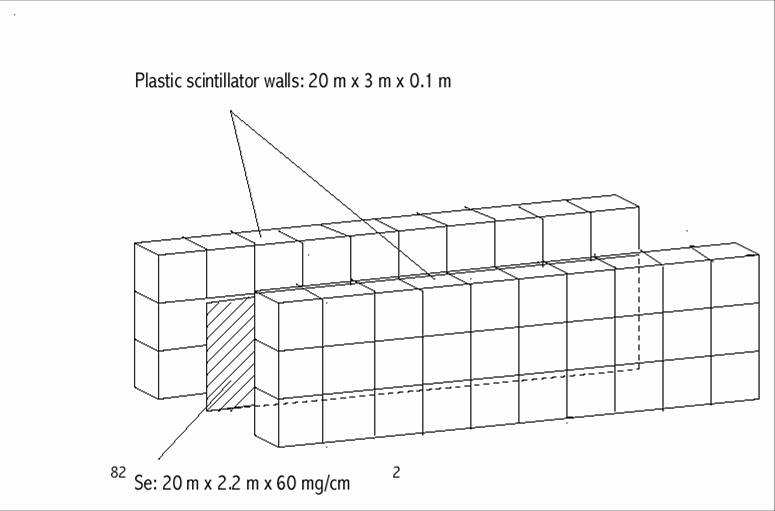
A new experiment of this type is currently in the planning stages and is known as SuperNEMO. If the proposal is given the go ahead then construction is expected to begin (location undecided) around 2008 with first runs expected around 2011. The design will be a simple Cartesian modular design, see figure. Each module will consist of a ββ emitter foil surrounded by a tracking volume and calorimeter walls. The calorimeters will contain large numbers of scintillators that can accurately measure energy deposition by energetic particles. Wires will be suspended through the tracking volume to track particle trajectories. The modular setup allows for easier construction on ground level and offers the possibility of altering the height, width and level proportions of each module - important flexibility in relation to the shape of the underground laboratory. Note also that this setup is independent of ββ source and plans can be altered if the theoretical community suggests that it should.
So by simply trying to make detections the experimental team introduce an efficiency term to the theoretical calculations. Then in order to obtain meaningful data, the efficiency needs to be calculated. The efficiency is a characteristic of a given experimental setup and therefore can only be determined by simulating the physics over a large number of events. Simulation is important not only for calculation of efficiencies but more generally allows for study of how the experimental setup behaves qualitatively and quantitatively; efficiency aside, simulation is an important part of the planning stages of any particle or nuclear experiment.
The programming involved is immense if performed from scratch for each experiment, even for the most basic. Geometries, materials, simulation of events and detection, statistical (Monte-Carlo) analyses, lists of processes and particles all have to be simulated and interact together properly. The importance of this task meant the continued development at CERN of a simulation tool known as Geant over the last thirty years. Over this time, vast libraries of processes and subroutines relating to all parts of a simulation have been built up and made available to the physics community.
Typically, a simulation consists of two files (although these can be incorporated as one), the source code that is compiled to produce an executable, and an include file that contains the libraries and common blocks. The libraries are all the sub-routines relating to the operation of the program or aspects of its simulation. The task of the simulator is then simply to call the right sub-routine at the right point in the main program and enter the appropriate parameters. The common blocks link together certain sub-routines that need to share certain parameters defined by the Geant code; the user being able to define their own in the main program. A generic source code will begin with all the program initialisations and general run commands, for example:
The geometry and materials are defined by the user after this as well as sub-routines to generate events and track the daughter particles and secondaries. Particles are tracked by a Monte-Carlo iteration procedure. Once a vertex is generated and initial momenta calculated, the particle is tracked by taking small steps - at the end of each step decisions are made based upon the particle's location, energy and physics processes in operation to determine its trajectory from that point onwards. This process continues step-by-step until the particle leaves the geometry, loses all its energy or the program encounters a problem with the code which leads to rejection of an event. The user can record energy deposited by each particle or in total and define an appropriate output or analysis thereof. The program will finish by giving instructions on how to output the data. In reality, the code is more extensive than this with complicated geometries and kinematics. Typically many sub-routines will be used even for basic geometries - either Geant or user defined.
The Fortran language has served the scientific community well, but it is only they that use it. The future of programming is in Object-Oriented (OO) languages which, although more painful to write, are more versatile for a number of reasons. A Geant 4 simulation code will contain the following components:
This may seem considerably more complicated (it is!), but for complex programs it is a more powerful approach. The key to this lies in the idea of a class. Programs of all types deal with many pieces of information, but it is how this information is brought to together that matters. Draw an analogy with a bank holding personal data concerning their clients. A record is held in a database where various pieces of information are held together where apart they would not make any sense. The structure in C++ that groups together all the data/information to describe a single object is known as a class. All the classes relating to a certain part of the C++ simulation are then held together in appropriate header files (like the include file in Fortran) which are called where necessary. Splitting the code up like this means that different sections of the code can be developed independently of each other; when they need to interact, the appropriate header file is included in the code. This also means that compilation can be speeded up after the first run. Each separate piece of source code is compiled separately so if a change is made only the code containing the change needs to be recompiled. It also means that getting the overall code correct is incredibly difficult for complicated programs (which Geant 4 simulations are) and are considerably longer (and hence slower initially) than Geant 3.2.1 codes.
As a general rule, all scientific computing is looking to move towards OO languages as Fortran becomes obsolete and neglected. The problem with OO languages is that they have not had the long run that Fortran has and so where vast libraries need to be built up (as in the case of Geant simulations), bugs are rife. The code has yet to tested to across the board of possible simulations; for example, Geant has only be tested on high energy experiments. Neutrinoless double beta decay is a low energy experiment with electron energies of the order MeV. It will take time to develop Geant 4 to the level that the Fortran versions have been to.
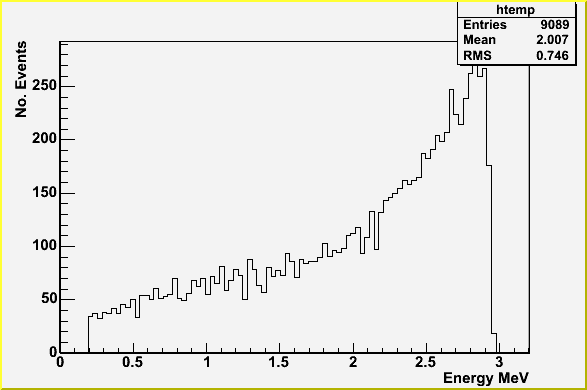
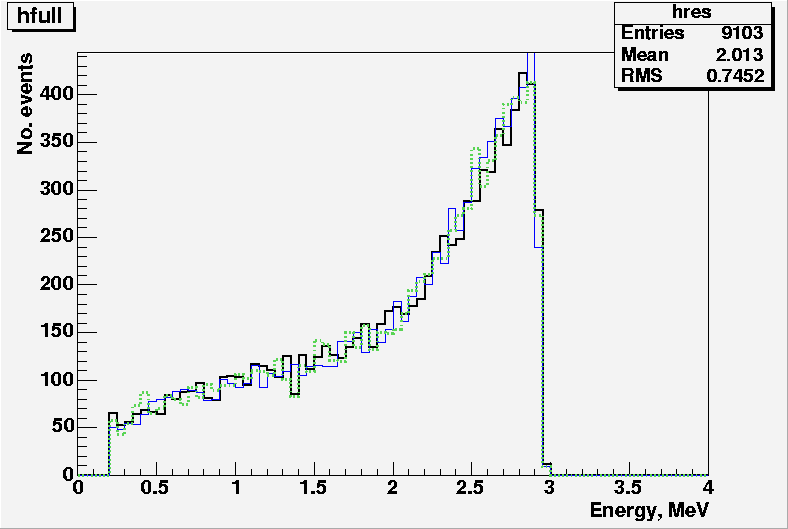
The graph to the left shows the energy spectrum for two simulated electrons. In a neutrinoless double beta decay the electrons take all the energy available from decay and so the theoretical spectrum should be a delta-function spike at the Q-value (available energy). The tail in the spectrum indicates that energy is being lost - due to the passage through the selenium and electrons not travelling perpendicular to the source.
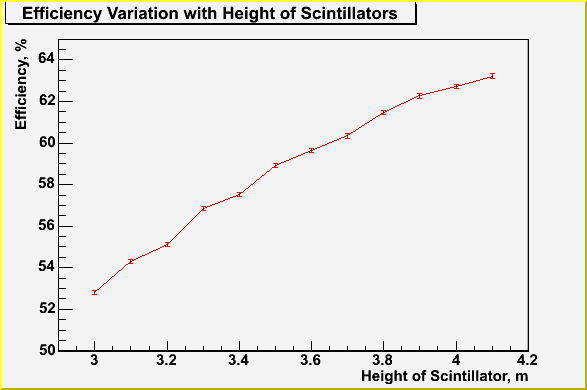
The graph to the right displays the effect of increasing the height of the scintillator walls on the detector efficiency. The generic setup has an effciency of 53 % which increases to 63 % when the height of the wall is 4 m. Many events are lost due to there being no walls, roof and sides - these being tricky to incorporate into detector design. By increasing the coverage by scintillator height, lost effciency can be clawed back. For the record, a setup with roof was simulated and an effciency of 75 % obtained. Therefore half the lost effciency has be reclaimed.
