W bosons can have helicity ![]() or 0.
A W boson with helicity
or 0.
A W boson with helicity ![]() 1 is said to be transversely polarised and one
with zero helicity is longitudinally polarised. This means that there are four
possible final polarised states of the W boson pair; transverse-transverse
(TT), longitudinal-longitudinal (LL), transverse-longitudinal (TL) and
longitudinal-transverse (TL).
1 is said to be transversely polarised and one
with zero helicity is longitudinally polarised. This means that there are four
possible final polarised states of the W boson pair; transverse-transverse
(TT), longitudinal-longitudinal (LL), transverse-longitudinal (TL) and
longitudinal-transverse (TL).
Of the final helicity combinations, all may be produced by both the s-channel and t-channel
processes, except the final state where the W bosons have opposite helicity
![]() 1 and
1 and ![]() 1. These two final
helicity states have angular momentum
1. These two final
helicity states have angular momentum ![]()
![]()
![]() and are only accessible
through
the t-channel neutrino exchange process.
and are only accessible
through
the t-channel neutrino exchange process.
It is
possible to write the helicity amplitude for
![]() in terms of the t-channel
neutrino exchange process and the s-channel TGC processes, including all
14 couplings parameters. For a final helicity state
in terms of the t-channel
neutrino exchange process and the s-channel TGC processes, including all
14 couplings parameters. For a final helicity state
![]() ,
where
,
where ![]() is the helicity of the
is the helicity of the
![]() and
and
![]() that of the
that of the
![]() ,
and
with initial helicity of the electron
,
and
with initial helicity of the electron
![]() , (In
the limit of massless leptons, the helicity of the positron is
, (In
the limit of massless leptons, the helicity of the positron is
![]() ), the helicity amplitude is given as:
), the helicity amplitude is given as:
![]() is the square of the centre-of-mass energy and
is the square of the centre-of-mass energy and
![]() is the
angle between the electron direction and the
is the
angle between the electron direction and the
![]() direction in the centre of
mass frame, known as the W production angle.
direction in the centre of
mass frame, known as the W production angle. ![]() is the four-momentum transfer
and is given by,
is the four-momentum transfer
and is given by,
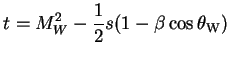 |
(3.19) |
where,
| (3.20) |
Equation 3.18 for the helicity amplitude consists of three
parts. The first, denoted by superscript ![]() is for W-pair production
through neutrino exchange. The second and third are for W-pair production through
photon and
is for W-pair production
through neutrino exchange. The second and third are for W-pair production through
photon and
![]() decays, and are denoted by superscript
decays, and are denoted by superscript ![]() and Z respectively. The
TGC parts are each summed over the seven possible couplings given in the
Lagrangian, equation 3.1. The
and Z respectively. The
TGC parts are each summed over the seven possible couplings given in the
Lagrangian, equation 3.1. The ![]() s are the terms which carry
the dependence on the coupling value and hence there are seven each for the
photon and
s are the terms which carry
the dependence on the coupling value and hence there are seven each for the
photon and
![]() TGCs. The
TGCs. The
![]() s give the helicity composition and W production angle for each of the
different coupling terms, note that these are the same for the photon and
s give the helicity composition and W production angle for each of the
different coupling terms, note that these are the same for the photon and
![]() TGC for each respective
TGC for each respective ![]() .
.
The explicit expressions for each of the ![]() s and
s and ![]() s can be calculated from
the Feynman diagrams and written in terms of the couplings given in
equation 3.1 [36,41,65]. They are shown in table 3.2, where in the
s can be calculated from
the Feynman diagrams and written in terms of the couplings given in
equation 3.1 [36,41,65]. They are shown in table 3.2, where in the
![]() propagator,
propagator, ![]() is approximated at
is approximated at
![]() to be:
to be:
| (3.21) |
and
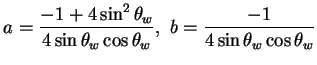 |
(3.22) |
The first column of table 3.2 gives the ![]() s given in equation 3.183.3. The first row is for the neutrino exchange
process. Due to the standard V
s given in equation 3.183.3. The first row is for the neutrino exchange
process. Due to the standard V![]() A constraint, the first term in this row will
be zero when the electron spin
A constraint, the first term in this row will
be zero when the electron spin
![]() .
.
To calculate the total amplitude for a certain helicity combination you must multiply each term
in the first column with the corresponding term in the column denoted with the
required helicity. Each product must be summed together, then the final sum
multiplied with the term at the top of the corresponding column. For helicity
combinations with
![]() and
and
![]() , the last column can be
used with
, the last column can be
used with
![]() ,
,
![]() and
and
![]() .
.
So, for example, the Standard Model amplitude,
![]() , for a pair of W bosons with spin
, for a pair of W bosons with spin
![]() , with the
initial electron spin
, with the
initial electron spin
![]() , would be:
, would be:
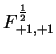 |
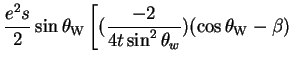 |
(3.23) | |
![$\displaystyle \left.(\frac{-2}{s}+\frac{2\cot\theta_{w}}{D_{Z}}(a+b))(-\beta)\right]$](img283.gif) |
The equivalent term for an initial electron spin of
![]() is
as in equation 3.24. Notice how the terms due to the neutrino
exchange are now absent due to the fact that right handed neutrinos cannot be
produced.
is
as in equation 3.24. Notice how the terms due to the neutrino
exchange are now absent due to the fact that right handed neutrinos cannot be
produced.
Another important thing to note from table 3.2 is the column for
W boson helicities
![]() , this shows explicitly that
these combinations can only be produced via the neutrino exchange process.
, this shows explicitly that
these combinations can only be produced via the neutrino exchange process.
 |
The W-pair production differential cross-section due to both the neutrino exchange and the TGC channels can be written in terms of the helicity amplitudes:
where the
![]() centre-of-mass momentum
centre-of-mass momentum
![]() .
.
As well as the total cross-section, predictions about the polarised cross-sections can also
be made,
for example, the production of pairs of transverse W bosons
![]() .
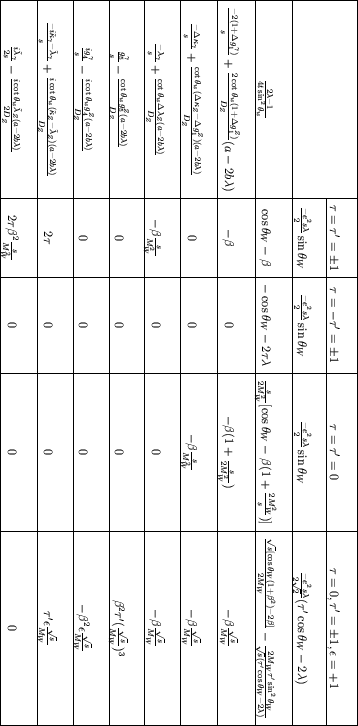
Figure 3.5 shows how the total cross-section and the total
polarised cross-sections behave as a function of centre-of-mass energy,
.
Figure 3.5 shows how the total cross-section and the total
polarised cross-sections behave as a function of centre-of-mass energy, ![]() . The range is from the threshold of W-pair production, through the energy
range of LEP-2 (162-202 GeV), and beyond.
. The range is from the threshold of W-pair production, through the energy
range of LEP-2 (162-202 GeV), and beyond.
 |
It can be seen that the total cross-section and each for the different polarisation
states rise rapidly from the threshold value, however, they all peak at
different values of ![]() , with the total cross-section for W-pair
production peaking at about 200 GeV. From table 3.2, it can be
shown that the cross-section for transverse-longitudinal (TL) W-pairs is always
equal to that of longitudinal-transverse (LT) W-pairs, even in the presence
of
anomalous couplings.
, with the total cross-section for W-pair
production peaking at about 200 GeV. From table 3.2, it can be
shown that the cross-section for transverse-longitudinal (TL) W-pairs is always
equal to that of longitudinal-transverse (LT) W-pairs, even in the presence
of
anomalous couplings.
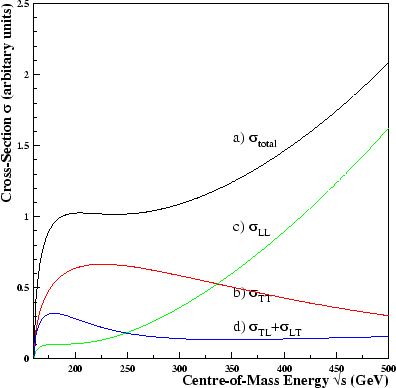 |
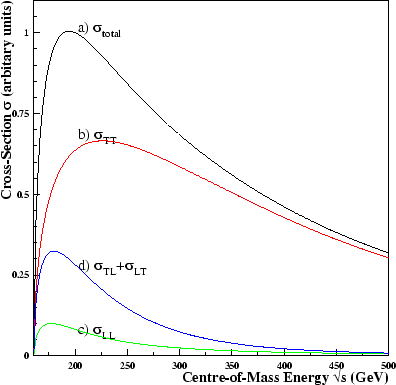
Figure 3.6 shows the total cross-sections as a function of
centre-of-mass energy in the presence of an anomalous coupling of
![]() =+1.
The cross-section blows-up with energy, which would
violate unitarity unless some non-Standard Model process occurs at some higher
energy value,
=+1.
The cross-section blows-up with energy, which would
violate unitarity unless some non-Standard Model process occurs at some higher
energy value,
![]() . With a non-zero
value of
. With a non-zero
value of
![]() , as the centre-of-mass energy increases the W-pairs produced
become almost entirely longitudinally polarised, so the dominant polarisation
state becomes LL. With the presence of any of
the anomalous couplings,
as
, as the centre-of-mass energy increases the W-pairs produced
become almost entirely longitudinally polarised, so the dominant polarisation
state becomes LL. With the presence of any of
the anomalous couplings,
as ![]() is increased, the polarisation of the W-pairs becomes dominated
by just one
of the polarisation states. Some of the polarisation states are completely
insensitive to certain
anomalous couplings.
Table 3.3 shows which polarisation
states are sensitive to which anomalous couplings and which state dominates
when
is increased, the polarisation of the W-pairs becomes dominated
by just one
of the polarisation states. Some of the polarisation states are completely
insensitive to certain
anomalous couplings.
Table 3.3 shows which polarisation
states are sensitive to which anomalous couplings and which state dominates
when ![]() becomes large.
becomes large.
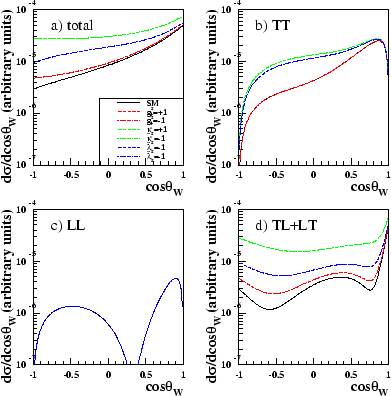
Plots of the differential cross-section of W-pair production as a function of the W production angle have been made at centre-of-mass energy
189 GeV, as this corresponds to the data sample considered in this thesis.
Figure 3.7 shows the
total differential cross-sections and polarised differential cross-sections for
the Standard Model and anomalous C and P-conserving couplings. The
anomalous couplings have been set at values ![]() 1.
1.
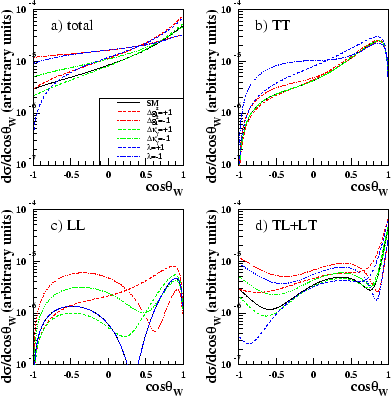 |
Figure 3.8 shows the total
differential cross-sections and polarised differential cross-sections for the
Standard Model and anomalous CP-violating
couplings. The anomalous couplings have been set at
values ![]() 1.
1.
Figures 3.7 and 3.8 show explicitly
the observations made in table 3.3, which were derived by looking
at table 3.2. It immediately can be seen that the LL differential
cross-section is insensitive to ![]() and all the CP-violating couplings.
TT is
insensitive to
and all the CP-violating couplings.
TT is
insensitive to
![]() and
and ![]() . For the CP-violating couplings the
negative coupling has an identical effect as the positive coupling.
. For the CP-violating couplings the
negative coupling has an identical effect as the positive coupling.
 |
By integrating over
![]() , the fraction of TT, LL and TL+LT W-pairs
can be calculated. This has been done for
figures 3.7 and 3.8 and the results are
displayed in table 3.4. Also shown in this table is the
proportion of each helicity state at a much higher energy than LEP-2 has run
at. This is to indicate once again which helicity state dominates the total
cross-section.
, the fraction of TT, LL and TL+LT W-pairs
can be calculated. This has been done for
figures 3.7 and 3.8 and the results are
displayed in table 3.4. Also shown in this table is the
proportion of each helicity state at a much higher energy than LEP-2 has run
at. This is to indicate once again which helicity state dominates the total
cross-section.