The $\chi ^{2}$ Fit to the Single W SDM Elements

The approach used is to perform a $\chi ^{2}$ fit between the SDM elements measured in the data with the predictions made using fully simulated Monte Carlo with different TGC values.

The simple form of a $\chi ^{2}$ [99] is given by:

$$\chi^{2} = \sum^{N}_{k=1}\left[\frac{y(x_{k})-f(x_{k};a)}{\sigma_{k}}\right]^{2}$$ (6.1)

Here $y(x_{k})$ is the measured value of an observable corresponding to a precise value of $x_{k}$, $\sigma_{k}$ is the error on that value and $f(x_{k};a)$ is the theoretical value corresponding to a precise value of $x_{k}$ and is a function of the parameter that is being measured, $a$. The $\chi ^{2}$ is formed by the sum over all the measured values, $k$, of the observables.

In this context $y(x_{k})$ is the measured value of the SDM element in bin $k$ of $\cos\theta_{\rm W}$. The theoretical value of the SDM element in bin $k$, corresponding to $f(x_{k};a)$, is a function of the TGC parameter being measured. The error, $\sigma_{k}$, is the standard deviation on the mean of the measured SDM element in bin $k$. The standard deviation on the mean is given by equation 6.2

$$\sigma_{k} = \sqrt{\frac{1}{N_{k}(N_{k}-1)}\sum^{N_{k}}_{i=1}\left(y(x_{k})_{i}-y(x_{k})\right)^{2}}$$ (6.2)

Where $y(x_{k})_{i}$ is the measured value from event $i$ and $y(x_{k})$ is the mean value of all events. In effect, the projection operator $\Lambda_{\tau\tau^{\prime}}$ applied to a single event gives the single measurement $y(x_{k})_{i}$. The form of equation 6.2 to calculate the statistical error on each SDM element for each bin of $\cos\theta_{\rm W}$ is therefore given by equation 6.3.

$$\sigma^{k}_{\tau\tau^{\prime}} = \sqrt{\frac{1}{N_{k}(N_{k}-1)}\s... ...ime}}(\theta^{*}_{i};\phi^{*}_{i})_{k} - \rho^{me}_{\tau\tau^{\prime}}(k))^{2}}$$ (6.3)

$\Lambda_{\tau\tau^{\prime}}(\theta^{*}_{i};\phi^{*}_{i})_{k}$ (i.e. $y(x_{k})_{i}$) represents the projection operators given in equation 4.1 and $\rho^{me}_{\tau\tau^{\prime}}(k)$ (i.e. $y(x_{k})$) is the calculated SDM element. The $\chi ^{2}$ given in equation 6.1 is formed by the sum over all observables. Each SDM element is separated into N bins of $\cos\theta_{\rm W}$, so effectively represents N observables. As there are nine SDM, it would also seem sensible to sum over all these, so the $\chi ^{2}$ would have the form shown in equation 6.4.

$$\chi^{2} = \sum^{N}_{k=1}\sum^{1}_{\tau=-1}\sum^{1}_{\tau^{\prime... ...)-\rho^{th}_{\tau\tau^{\prime}}(k;a)}{\sigma_{\tau\tau^{\prime}}(k)}\right]^{2}$$ (6.4)

Due to the hermitian nature of the spin density matrix, $\rho_{\tau\tau^{\prime}} = \rho^{*}_{\tau^{\prime}\tau}$, not all the elements of the matrix are independent observables. In fact, only the diagonal elements ($\rho_{++}$, $\rho_{--}$ and $\rho_{00}$) and three of the off-diagonal elements, $\rho_{+-}$ (= $\rho^{*}_{-+}$), $\rho_{+0}$ (= $\rho^{*}_{0+}$) and $\rho_{-0}$ (= $\rho^{*}_{0-}$) need be included in the $\chi ^{2}$ fit.

The diagonal matrix elements are purely real and so represent three observables. However, as seen earlier, $\rho_{+-}$, $\rho_{+0}$ and $\rho_{-0}$ are complex, so have both real and imaginary parts. Each of these then effectively represents 2 observables, the coefficient of the real part and that of the imaginary. This then totals nine observables to which the $\chi ^{2}$ fit can be performed:

$$\rho_{++},~ \rho_{--},~ \rho_{00}$$

$${\rm Re}(\rho_{+-}),~ {\rm Re}(\rho_{+0}),~ {\rm Re}(\rho_{-0})$$ (6.5)

$${\rm Im}(\rho_{+-}),~ {\rm Im}(\rho_{+0}),~ {\rm Im}(\rho_{-0})$$

The imaginary SDM observables are completely insensitive to the CP-conserving couplings and are therefore not used when fitting these couplings. When fitting the CP-violating couplings all nine observables are used.

The $\chi ^{2}$ given in equation 6.4 is a naive simplification that assumes each measured SDM element is completely uncorrelated from all the other SDM elements. All SDM elements in a $\cos\theta_{\rm W}$ bin are derived from the same data subset and are therefore correlated. The diagonal elements of the SDM are normalised to unity, so are highly correlated. Correlations between different bins of $\cos\theta_{\rm W}$ may be assumed to be negligible as they use different subsets of the data sample. The correlation can be included in equation 6.4 by introducing a covariance matrix, as shown in equation 6.6^6.1.

$$\chi^{2} = \sum^{N}_{k=1}\sum^{9}_{i=1}\sum^{9}_{j=1} \left[ \lef... ...}_{ij}(k)\right) \left( \rho^{me}_{j}(k)-\rho^{th}_{j}(k;a) \right) \right]^{2}$$ (6.6)

In equation 6.6 the $\rho_{i}$ and $\rho_{j}$ represent the nine SDM observables indicated in equation 6.5. The covariance matrix, $V_{ij}(k)$, is given by:

$$V_{ij}(k) = \omega_{ij}(k)\sigma_{i}(k)\sigma_{j}(k)$$ (6.7)

Where $\omega_{ij}(k)$ is the correlation between SDM observable $i$ and $j$ in bin $k$ of $\cos\theta_{\rm W}$. A statistical analysis can be applied to the data to directly calculate the covariance matrix:

$$V_{ij} = \frac{1}{N_{k}(N_{k}-1)} \left[ \sum_{\epsilon=1}^{N_{k}... ...heta^{*}_{\epsilon};\phi^{*}_{\epsilon})_{k} - \rho^{me}_{j}(k) \right) \right]$$ (6.8)

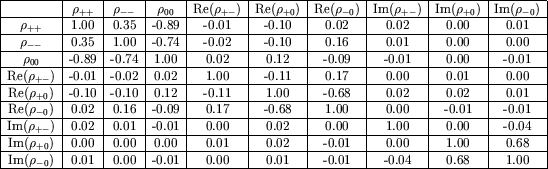
Table 6.1 shows the correlations between all the SDM observables in one bin of $\cos\theta_{\rm W}$, calculated from a SM sample of EXCALIBUR Monte Carlo data. The SDM elements were divided into eight equal bins in $\cos\theta_{\rm W}$. The results shown are for the first bin. The correlations for the other seven bins are of similar magnitude. It was found that the intra-bin correlations were negligible.

Table 6.1: The correlations between the $-1<$$\mbox{$\cos\theta_{\rm W}$}$$<-0.875$ bin of all the single W SDM observables used to calculate the TGCs. These values were calculated from a Standard Model four-fermion Monte Carlo sample.

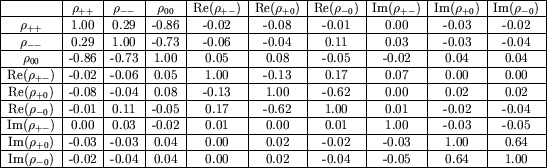
It was found that the correlations for non-Standard Model Monte Carlo were similar to those in table 6.1, although not identical. An example with Monte Carlo generated with an anomalous coupling of $\Delta g^{z}_{1}$=$-$2 is shown in table 6.2.

Table 6.2: The correlations between the $-1<$$\mbox{$\cos\theta_{\rm W}$}$$<-0.875$ bin of all the single W SDM observables used to calculate the TGCs. These values were calculated from a non-Standard Model four-fermion Monte Carlo sample with $\Delta g^{z}_{1}$$=-2.0$.