A measurement of the transverse momentum of Z-bosons and the associated W-mass uncertainty
Welcome Page
Page content:
1. Introduction
The Standard Model provides the backbone for nearly all of modern high-energy particle physics. Currently, the model's validity is heavily dependent upon the masses of W-boson and the top quark. Should the masses of these particles differ from the accepted values, it would indicate severe shortcomings in the Standard Model; new physics would be required. It is for this reason, that the masses are measured with as much accuracy and precision as possible.
One method of measuring the mass of the W-bosons involves colliding highly energetic beams of protons and anti-protons in particle accelerators. The mass of the W-boson can then be determined via observations of the leptonic decay products.

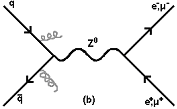
Figure 1: (a) A Feynman diagram for the creation of a W- boson. In a proton-antiproton collision, the quarks would be a down and an anti-up. (b) The similar process for the creation of a Z0 boson. The two quarks involved in a proton-antiproton collision could be an up/anti-up pair, or a down/anti-down pair. The radiation of gluons prior to collision is also depicted in both cases.
A problem arises as the energy is increased; the quarks become more likely to emit gluons prior to collision. The assumption that W± has no transverse momentum is now invalid, affecting the calculated mass. This problem cannot be easily rectified because one of the decay products is a neutrino, which is hard to detect. However, the Z-boson formation process is very similar to that of the W-boson. The decay products are electrons, positrons, and muons, all of which can be measured accurately.
A transverse momentum distribution for Z0 can then be derived from experimental data, and modified to describe W±. Having greater knowledge of how this momentum varies with energy should allow the uncertainty in mass of the W-boson to be reduced.
2. Aims
The aims of the project are:
- Understand the effect the gluon radiation has upon the kinematics of W and Z-boson production.
- Derive a form for the transverse momentum of Z0, by fitting experimental data with that of a detector simulation, and comparing it with the latest theoretical models.
- Estimate how the uncertainty in the W± mass is affected by the transverse momentum of Z0.
3. Planned Approach
3.1 Detector simulation
It is not possible to detect all events in a particle accelerator satisfactorily, thus a theoretical PT(Z) distribution will not agree with experiment data due to detector resolution effects; these effects are to be simulated.
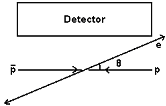
Figure 2: If the electrons/muons are scattered with a small angle, then they will miss the whole detector.
3.1.1 Limits on the scattering angle
The electronic calorimeters are of a finite length and therefore, it is possible that they will not detect events where the particles scatter with a small angle, such as depicted in figure 2.
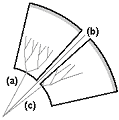
Figure 3: How different paths can affect the measurement. At (a), an electron passes into the centre of the calorimeter, an accurate measurement should result; the electon following (b) would not be measured at all by the calorimeter array, whereas the (c) electron would give a miseleading result, part of the shower has exited the device before measurement.
3.1.2 Limits on the radial angle of scatter
The CDF assembly uses a modular system of calorimeters, leaving small gaps between each module. However, this system can only measure accurately if the electrons enter the calorimeter near the middle of the module. Otherwise, not all of electron shower will be contained within, biasing the result. There is also the chance that the electron will radiate a photon before entering the calorimeter.
3.2 Fitting data
3.2.1 Comparing the CDF data with theory
The corrected form of PT(Z) is to be fitted against CDF data. A data analysis package such as JRoot is to be used; JRoot is the Root package rewritten from C++ into Java. The form of the PT(Z) distribution will be iterated so that it is consistent with the experimental data.
3.2.2 Estimating the uncertainty in the mass of the W-boson
The form of the PT(W) will be constrained to fit the CDF-corrected PT(Z) distribution. The W± formationprocesses at the Tevatron are similar to the Z0 formation processes, yet the differences in the kinematics will need to be accounted for.
3.3 Possible problems
As with all tasks that require large amounts of programming, standard problems may arise: unforeseen bugs at a code level, run-time errors, etc. These will have to be identified and corrected as they appear. However, one of the largest problems to be overcome is the detector simulation; whether the enforced cuts on the data are within bounds of relative acceptance must be considered.