2.7 Luminosity spectra

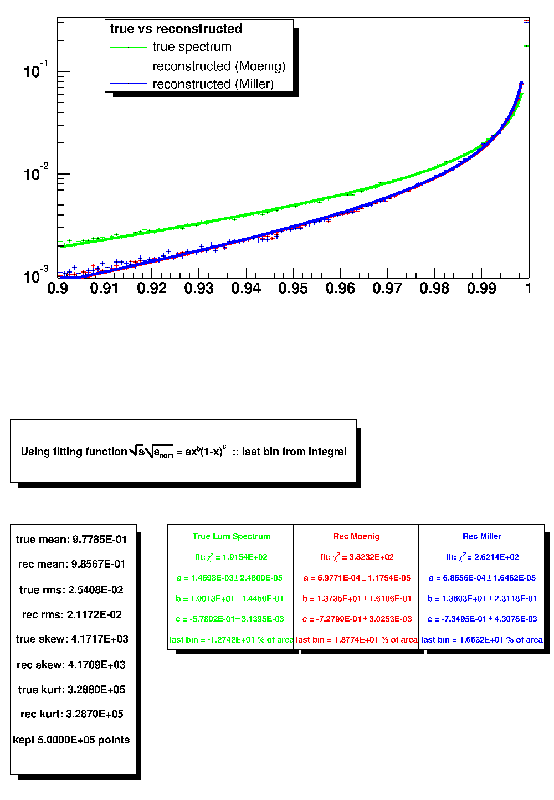
A full luminosity spectrum can then be produced. The true √S for each event is evaluated from the 4-momenta. The scattering angles are calculated from the dot products of the 3D momenta, and thus we can evaluate √S_est, the estimated centre of mass energy. The Luminosity Spectrum, ∂L/∂√S, is the distribution of √S for all events.

The curves are plotted along with the lines of best fit, and the fit parameters, as well as the statistical moments of the curves, are outputted. We only output the curves from 90% of the energy upwards, as below this region the calorimeter has enough resolution to evaluate the centre of mass energy of an event, and the effect of the lower tail of the spectrum is limited, due to the low number of events.

2.7.1 Curve Fitting methods

The curve fitting equation is non-standard: it is given by equation 1 above.

We use the in-built Root chi-squared fitting classes.

We find that a convergence can usually never be found if the whole histogram is to be fitted: the (1-x)^a is too sharply peaked at 1, and the dirac delta function then needs a negative coefficient effectively model the peak. After several attempts at using gaussians and exponentials, as well as other mathematical devices to avoid singularities, an empirical method is settled for: the luminosity spectrum histogram is fitted up to the last bin, with a simpler version of equation (1), and the last bin can then be calculated from normalisation (as the area of the spectrum is normalised to 1.)

This has the advantage of giving a very close fit, and of directly giving value of the last bin , which is an important physical quantity (fraction of particles within 0.1% of nominal energy.)

The function we use is of the form:

, where a, b and c are fitting parameters, and a 4^th parameter d is the value of the last bin, and is obtained from the normalisation of the area under the curve.