2.8 Corrections methods

Two things can be noted about the spectra in figure m: the two reconstructed curves, in red and green, are very close. They are also quite far from the true luminosity spectrum, as they are more sharply peaked: this implies that there is more energy loss than is being accounted for by the reconstruction, as the curves are broader.

Both reconstructions assume the following:

--one photon emitted only

--photon is emitted along the beam axis

--the acolinearity is small

--the outgoing electron and positron angles are in the region 0.1 < θ < 0.3

--the outgoing e+ and e- are on the same plane

The procedure we apply ourselves to is to look for the conditions that the reconstructions give an accurate fit of the true luminosity spectrum.

2.8.1 Filtering angles

The first step is to apply angle cuts to the standard accelerator spherical coordinates angles.

In all subsequent images, the following angle cuts are applied : 0.1 < θ₁ < 0.3 , 0.1 < θ₂ < 0.3. This is a realistic angle cut for the reconstruction, which would use the forward tracking detector in TESLA.

This is best exemplified in figures n, o below. Notice also the intrinsic bhwide angle cut: no particles are emitted below θ = 0.11 radians even in the uncut phase space in figure n.

Figures n, o: reduction of θ phase space

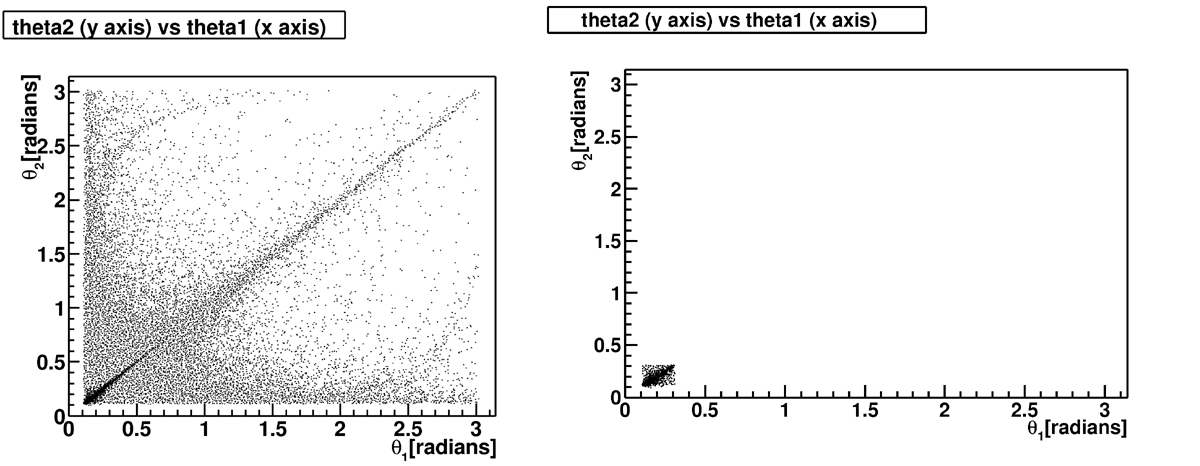
Figure n: θ phase space before angle cuts------- Figure o: θ phase space after angle cuts

Applying angle cuts on theta alone marginally improves the reconstructions, and exposes the difference in reconstruction methods.

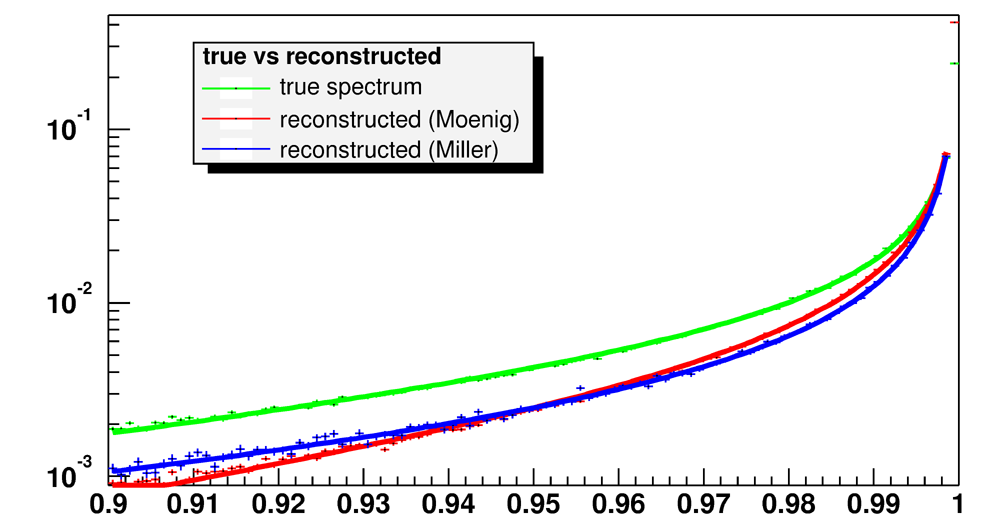
Figure p: luminosity spectrum with theta angle cuts

We also attempt to restrict the acoplanarity by also filtering out events with a large φ angle difference, but we find that

a.) the φ₁ and φ₂ angle distributions are random , between -π and π and

b.) the vast majority of events are co-planar, i.e. have the same φ angle.

2.8.2 Number of photons radiated

The number of radiated photons can be obtained from our modified version of bhwide. We restrict the analysis to events where one or less photons have been emitted. This, if combined with the theta cuts above, dramatically improves the reconstruction, especially that proposed by Frary-Miller, where:

--the proportion of events in the last bin is now found accurately (which is crucial for the top cross section smearing, cf section 2.9.2)

--the reconstruction is good in the region above with energy above 97% of nominal energy, which is precisely that where the calorimeter lacks in resolution.

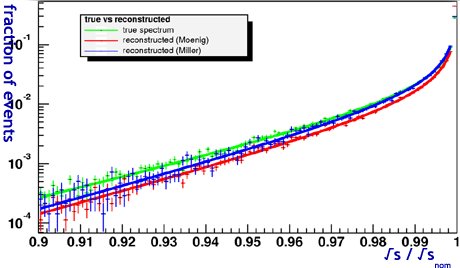
Figure q: luminosity spectrum for events with less than two photons radiated

2.8.3 Correlated dispersion

One of the original questions asked was: "Does correlated momentum loss compensate for momentum mismatch?"

To test this, we artificially 'decorrelate': we force bhwide, the collision program, to choose electrons and positrons from different positions within the beam created by guinea-pig.

Whilst this does not dramatically increase the accuracy of the last bin content, it improves the reconstruction in the region below 97% of nominal energy, which can be subject to calorimeter testing.

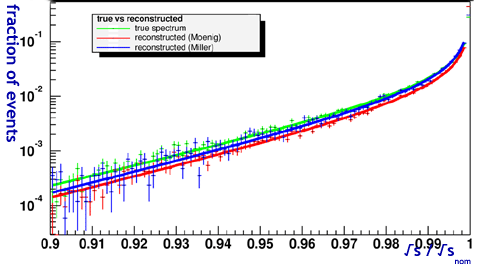
Figure q: luminosity spectrum for events with less than two photons radiated