Constraining the Number of Parameters

Considering terms with operators up to dimension six gives the 14 TGCs in equation 3.1. However, further constraints can be made to the theory, by taking into consideration physical effects seen in other experimental data. Precise measurements made at LEP-1 on the ${\rm Z}^{0}$ resonance [48,49,50,51] support embedding any anomalous terms in an ${\rm SU}(2)_{L}\times {\rm U}(1)_{Y}$ gauge invariant structure [36].

By enforcing ${\rm SU}(2)_{L}\times {\rm U}(1)_{Y}$ gauge invariance and considering only operators up to dimension six [52], the TGC New Physics (NP) Lagrangian can be expressed in terms of the unmixed fields, the $W^{3}B$ base [36,42], as in equation 3.8.

$${\cal{L}}_{TGC} = g^{\prime}\frac{\alpha_{B\phi}}{M^{2}_{W}}{\cal{O}}_{B\phi} + g\f... ...\phi}}{M^{2}_{W}}{\cal{O}}_{W\phi} + g\frac{\alpha_{W}}{M^{2}_{W}}{\cal{O}}_{W}$$

$$+ \frac{gg^{\prime}}{2}\frac{\tilde{\alpha}_{BW}}{M^{2}_{W}}\tilde{\cal{O}}_{BW} + g\frac{\tilde{\alpha}_{W}}{M^{2}_{W}}\tilde{\cal{O}}_{W}$$ (3.8)

Where $e = g\sin\theta_{w}= g^{\prime}\cos\theta_{w}$. The $\cal{O}$ are the operators capable of inducing the TGC NP couplings. The explicit form of the CP-conserving operators are given by equation 3.9 and the CP-violating are given by equation 3.10

$${\cal{O}}_{B\phi} = iB^{\mu\nu}(D_{\mu}\Phi)^{\dagger}(D_{\nu}\Phi)$$

$${\cal{O}}_{W\phi} = i(D_{\mu}\Phi)^{\dagger}{\boldsymbol{\tau}}\cdot{\bf W}^{\mu\nu}(D_{\nu}\Phi)$$ (3.9)

$${\cal{O}}_{W} = \frac{1}{3!}({\bf W}^{\mu}_{~\rho} \times {\bf W}^{\rho}_{~\nu}) \cdot {\bf W}^{\nu}_{~\mu}$$

$$\tilde{\cal{O}}_{BW} = \Phi^{\dagger}\frac{\boldsymbol{\tau}}{2}\cdot\tilde{\bf W}^{\mu\nu}\Phi B_{\mu\nu}$$

$$\tilde{\cal{O}}_{W} = \frac{1}{3!}({\bf W}^{\mu}_{~\rho} \times {\bf W}^{\rho}_{~\nu}) \cdot \tilde{\bf W}^{\nu}_{~\mu}$$ (3.10)

where

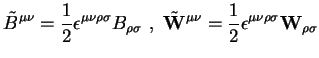$$\tilde{B}^{\mu\nu} = \frac{1}{2}\epsilon^{\mu\nu\rho\sigma}B_{\rh... ...de{\bf W}^{\mu\nu} = \frac{1}{2}\epsilon^{\mu\nu\rho\sigma}{\bf W}_{\rho\sigma}$$ (3.11)

the $\boldsymbol{\tau}$ are the Pauli matrices, which represent the generators of the SU$(2)$ group and $\Phi$ is the Higgs doublet. $B_{\mu\nu}$ is the U$(1)_{Y}$ gauge field strength, ${\bf W}_{\mu\nu}$ is the SU$(2)_{L}$ gauge field strength and $D_{\mu}$ is the ${\rm SU}(2)_{L}\times {\rm U}(1)_{Y}$ covariant derivative. All of these are given below, (3.12), (3.13) and (3.14).

$$B_{\mu\nu} = \partial_{\mu}B_{\nu} - \partial_{\nu}B_{\mu}$$ (3.12)

$${\bf W}_{\mu\nu} = \partial_{\mu}{\bf W}_{\nu} - \partial_{\nu}{\bf W}_{\mu} - g{\bf W}_{\mu} \times {\bf W}_{\nu}$$ (3.13)

$$D_{\mu} = \partial_{\mu} + ig\frac{\boldsymbol{\tau}}{2}\cdot{\bf W}_{\mu} + ig^{\prime}YB_{\mu}$$ (3.14)

In the covariant derivative, $Y$ is the hypercharge of the field upon which $D_{\mu}$ is acting. The $\alpha_{i}$ parameters in equation 3.8 can then be written in terms of the TGC parameters given in equation 3.1:

$$\alpha_{W\phi} = \cos^{2}\theta_{w}\Delta g^{z}_{1}$$

$$\alpha_{B\phi} = \Delta\kappa_{\gamma} - \Delta g^{z}_{1}\cos^{2}\theta_{w}$$

$$\alpha_{W} = \lambda$$ (3.15)

$$\tilde{\alpha}_{BW} = \tilde{\kappa}_{\gamma}$$

$$\tilde{\alpha}_{W} = \tilde{\lambda}_{\gamma}$$

with the constraints:

$$\Delta\kappa_{z} = \Delta g^{z}_{1} - \tan^{2}\theta_{w}\Delta\kappa_{\gamma}\;\;\;\;\;\;\;\;$$

$$\lambda = \lambda_{\gamma} = \lambda_{z}$$

$$\tilde\kappa_{z} = -\tan^{2}\theta_{w}\tilde\kappa_{\gamma}$$ (3.16)

$$\tilde\lambda_{z} = \tilde\lambda_{\gamma}$$

Where the $\Delta$ indicates the deviation from their Standard Model value, so $\Delta g^{z}_{1}$$=$ $g^{z}_{1}$$- 1$ and $\Delta\kappa_{\gamma}$$=$ $\kappa_{\gamma}$$- 1$.

Not all 14 TGC parameters from equation 3.1 were included in this ${\rm SU}(2)_{L}\times {\rm U}(1)_{Y}$ gauge invariant constraint. The couplings that violate charge conjugation symmetry, $g^{\gamma}_{4}$, $g^{\gamma}_{5}$ and the analogous Z couplings, have been ignored. This is because, as mentioned earlier, without the intervention of higher order operators, if the photon couplings were non-vanishing at $q^{2}=0$ they would violate electromagnetic gauge invariance. However, similar constraints through ${\rm SU}(2)_{L}\times {\rm U}(1)_{Y}$ gauge symmetry can be put on the charge conjugation violating parameters [53,54], for example, the constraint on $g^{\gamma}_{4}$ and $g^{z}_{4}$ is shown in equation 3.17.

$$\mbox{$g^{z}_{4}$} = \mbox{$g^{\gamma}_{4}$}$$ (3.17)

We have considered both CP-conserving and CP-violating anomalous couplings within the Lagrangian, and embedded them in a ${\rm SU}(2)_{L}\times {\rm U}(1)_{Y}$ gauge invariant structure. However, there is very good experimental evidence from the measurement of the neutron electric dipole moment [55,56], against the existence of a CP-violating electromagnetic interaction. Also, bounds on the W Boson electric dipole moment [57], which is related to the CP-violating photon TGCs, equation 3.6, would suggest that the existence of an anomalous CP-violating photon TGC is unlikely. However, these measurements do not constrain the C-violating coupling, $g^{\gamma}_{4}$, as highly as they do the P-violating couplings [58]. LEP1 data also suggests that ${\rm SU}(2)_{L}\times {\rm U}(1)_{Y}$ symmetry holds to very high precision.

All this would then suggest that the possibility of a CP-violating TGC as highly unlikely and thus the 14 TGC parameter set can be reduced to just three parameters; $\Delta\kappa_{\gamma}$, $\Delta g^{z}_{1}$ and $\lambda$. However, few direct limits have been placed on the CP-violating couplings. Values for all the CP-violating TGCs have been reported by the ALEPH collaboration [59,60], and for $\tilde{\kappa}_{z}$ and $\tilde{\lambda}_{z}$ by the DELPHI collaboration [63]. Values of $\tilde{\kappa}_{\gamma}$ and $\tilde{\lambda}_{\gamma}$ have been reported by D0 collaboration from the process ${ \rm p}\bar{\rm p} \rightarrow \ell\nu\gamma + {\rm X}$ [61,62]. All these sets of results do not constrain the couplings to ${\rm SU}(2)_{L}\times {\rm U}(1)_{Y}$ gauge invariance.

The set of couplings measured in this thesis will all require the ${\rm SU}(2)_{L}\times {\rm U}(1)_{Y}$ gauge symmetry constraints, but will not be constrained to CP-invariance, and so are as follows; $\Delta\kappa_{\gamma}$, $\Delta g^{z}_{1}$, $\lambda$, $\tilde{\kappa}_{z}$, $\tilde{\lambda}_{z}$ and $g^{z}_{4}$.