CPT and CP-Invariance

At tree level, for the helicity amplitudes, CPT-invariance implies [67] that,

$$F^{\lambda}_{\tau_{1}\tau_{2}}(s,\cos\theta_{\rm W}) = \left(F^{\lambda}_{-\tau_{2}-\tau_{1}}(s,\cos\theta_{\rm W})\right)^{*}$$ (3.39)

The consequences of this for the single W SDM elements are:

$$\rho^{W^{-}}_{\tau\tau^{\prime}}(s,\cos\theta_{\rm W}) = \left(\rho^{W^{+}}_{-\tau-\tau^{\prime}}(s,\cos\theta_{\rm W})\right)^{*}$$ (3.40)

The off-diagonal elements of the single W SDM are complex in nature, so if equation 3.40 is broken down into the real and imaginary parts, the following two relations are obtained:

$$Re\left(\rho^{W^{-}}_{\tau\tau^{\prime}}(s,\cos\theta_{\rm W})\right) - Re\left(\rho^{W^{+}}_{-\tau-\tau^{\prime}}(s,\cos\theta_{\rm W})\right) = 0$$ (3.41)

$$Im\left(\rho^{W^{-}}_{\tau\tau^{\prime}}(s,\cos\theta_{\rm W})\right) + Im\left(\rho^{W^{+}}_{-\tau-\tau^{\prime}}(s,\cos\theta_{\rm W})\right) = 0$$ (3.42)

The behaviour of the real parts for the single ${\rm W}^{-}$ and single ${\rm W}^{+}$ SDM elements can be seen in figure 3.11 and thus equation 3.41 is confirmed, even in the presence of anomalous couplings.

As mentioned earlier, at tree level, for a CP-invariant reaction, the helicity amplitudes fulfill the following relation:

$$F^{\lambda}_{\tau_{1}\tau_{2}}(s,\cos\theta_{\rm W}) = F^{\lambda}_{-\tau_{2}-\tau_{1}}(s,\cos\theta_{\rm W})$$ (3.43)

Thus the single W SDM elements for the ${\rm W}^{-}$ would then be related to those for the ${\rm W}^{+}$ as follows:

$$\rho^{W^{-}}_{\tau\tau^{\prime}}(s,\cos\theta_{\rm W}) = \rho^{W^{+}}_{-\tau-\tau^{\prime}}(s,\cos\theta_{\rm W})$$ (3.44)

Like equation 3.40, equation 3.44 has some important implications. Splitting the single W SDM elements into their real and imaginary parts once again, for the real parts equation 3.44 reproduces equation 3.41 which was brought about by CPT-invariance. However, for the imaginary parts the following is now true,

$$Im\left(\rho^{W^{-}}_{\tau\tau^{\prime}}(s,\cos\theta_{\rm W})\right) - Im\left(\rho^{W^{+}}_{-\tau-\tau^{\prime}}(s,\cos\theta_{\rm W})\right) = 0$$ (3.45)

Combining equations 3.40 and 3.44 brings about a simple, but extremely important conclusion. At tree level in a CP-invariant interaction, the imaginary parts of all SDM elements are zero. Any deviation in the imaginary parts could only occur in the presence of CP-violation. Thus, this means that equation 3.45 gives a sensitive test of tree level CP-violation within weak bosonic self interactions. As CP and CPT-invariance give the same relations for the real parts of the SDM elements, then the real parts do not provide for sensitive tests of CP-invariance.

In the presence of CP-violation at tree level, the magnitude by which equation 3.45 differs from zero is given by:

$$Im\left(\rho^{W^{-}}_{\tau\tau^{\prime}}(s,\cos\theta_{\rm W})\right) - Im\left(\rho^{W^{+}}_{-\tau^{\prime}-\tau}(s,\cos\theta_{\rm W})\right)$$

$$= 2Im\left(\rho^{W^{-}}_{\tau\tau^{\prime}}(s,\cos\theta_{\rm W})\right)$$ (3.46)

$$= -2Im\left(\rho^{W^{+}}_{-\tau-\tau^{\prime}}(s,\cos\theta_{\rm W})\right)$$

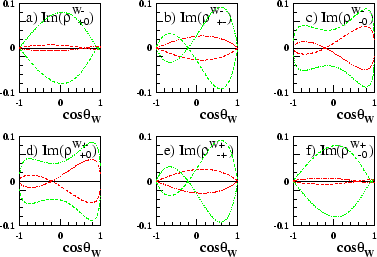
Figure 3.13 shows the imaginary parts of the off-diagonal elements of the single W SDM. It can immediately be seen that in the absence of CP-violation all these elements are zero. The plots with CP-violating couplings implemented verify the nature of the elements described by equation 3.46. Figure 3.13 also demonstrates that a matrix element with a positive CP-violating coupling implemented, is equal to the negative of the same matrix element with a negative CP-violating coupling implemented. With the real parts of the SDM elements there is no difference seen between a negative and positive CP-violating coupling of equal magnitude.

Figure 3.13: Examples of the imaginary parts of the off-diagonal single W SDM elements. The solid black line is the Standard Model case. The red lines are for CP-violating anomalous coupling $\tilde{\kappa}_{z}$ and the green line is for CP-violating anomalous coupling $\tilde{\lambda}_{z}$. The dotted (dashed) line indicates a coupling of $+$1 ($-$1).

These relationships will break down in the face of effects beyond tree-level. The presence of loop effects, both CP-conserving and CP-violating will always cause the imaginary parts of the SDM elements to deviate from zero [67]. However, these deviations, unlike tree level CP-violation, cause both the ${\rm W}^{-}$ and ${\rm W}^{+}$ elements to deviate from zero in the same way. So suitable combinations of SDM elements can be formed in which deviations due to loop effects cancel, these are shown in equation 3.47. Any deviation from these equations could only be due to tree level CP-violation and so give a genuine and sensitive test of CP-violation [36,67].

$$Im(\rho^{W^{-}}_{+-}) - Im(\rho^{W^{+}}_{-+}) = 0$$

$$Im(\rho^{W^{-}}_{+0}) - Im(\rho^{W^{+}}_{-0}) = 0$$ (3.47)

$$Im(\rho^{W^{-}}_{-0}) - Im(\rho^{W^{+}}_{+0}) = 0$$

Conversely, combinations of matrix elements may be formed to test for loop effects in which effects due to CP-violation cancel. These are derived from equation 3.42 and are shown explicitly in equation 3.48. Any deviations from these could only be an indication of effects beyond tree-level or the presence of CPT-violation.

$$Im(\rho^{W^{-}}_{+-}) + Im(\rho^{W^{+}}_{-+}) = 0$$

$$Im(\rho^{W^{-}}_{+0}) + Im(\rho^{W^{+}}_{-0}) = 0$$ (3.48)

$$Im(\rho^{W^{-}}_{-0}) + Im(\rho^{W^{+}}_{+0}) = 0$$