



Next: Events with Final States
Up: Application to Data Events
Previous: Calculating the Polarised Cross-Sections
Contents
When looking at the Monte Carlo data samples, it was assumed that the
angular distributions of all four of the decay fermions are well known and
that each individual fermion is perfectly identified. This is not the case with
real data. There are three possible decay
channels of the W-pair. The leptonic (4.8), the hadronic (4.9) and the semi-leptonic (4.10). Each of these posses their own
distinct signatures.
Each final fermion type has its own difficulties associated with it when trying to measure them. A brief
description of these are given below. A full discussion on event selection and
reconstruction is given in chapter 5.
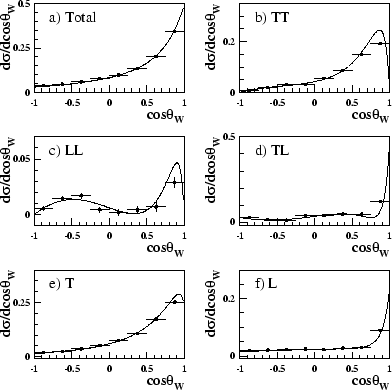
Figure 4.4:
The differential cross-sections for different W boson helicity states calculated from Standard Model Monte Carlo. a) is the total differential cross-section. b) is for the production of two transversely polarised W bosons. c) is for the production of two longitudinally polarised W bosons. d) is for the production of a longitudinal and a transverse W boson. e) and f) are for the production of at least one transverse and one longitudinal W boson in the pair respectively. Overlaid on all the plots is the analytical prediction for the Standard Model.
 |
- The massless neutrino cannot be detected and passes
straight through without leaving any signal.
- The hadrons produce jets of hadronic particles,
making identification of charge, and therefore differentiating between fermion and anti-fermion very difficult indeed.
- If the lepton is a
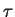 it will decay before it is
detected.
It can decay into a lighter lepton and neutrinos or into hadronic particles. In
all cases reconstruction of direction will be made difficult.
it will decay before it is
detected.
It can decay into a lighter lepton and neutrinos or into hadronic particles. In
all cases reconstruction of direction will be made difficult.
These differences in the way each fermion behaves then mean that each decay channel has its own set of
difficulties associated with it when trying to reconstruct the W production and
decay angles.
- The fully leptonic decay is measured as two leptons.
So, although the lepton and anti-lepton are identified, the fact that not
all the momentum
is measured immediately complicates things. There will always be a two fold
ambiguity within the calculation of the W production angle.
All the missing momentum is assumed to be that of the two neutrinos.
If there is any Initial State Radiation,
the assumed
four-momentum of the neutrinos will actually be that of the neutrinos plus
the ISR photon. The production
four-momentum of the W boson will then be calculated incorrectly and so leads to incorrect
calculation of the
the decay angles in the W rest frame. The problem will
be further enhanced if one or both of the leptons are taus.
- The fully hadronic decay produces four jets of particles. All
the the momentum components of the four jets will be measured, but there is
still a three-fold problem. Firstly, each hadron has to be assigned to the
correct jet. This can be done by, for example, using the Durham
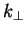 algorithm [68,69,70,71] to force
each selected event into four jets. Once this has been done the correct di-jet
combination has to be identified, i.e. the two jets from each W boson have to
be paired together. This is possible by using a likelihood
algorithm [72]. Both these processes are not 100% efficient.
The charge of each jet is unknown, making it very difficult
to distinguish between the particle and anti-particle from each W boson and
even the
algorithm [68,69,70,71] to force
each selected event into four jets. Once this has been done the correct di-jet
combination has to be identified, i.e. the two jets from each W boson have to
be paired together. This is possible by using a likelihood
algorithm [72]. Both these processes are not 100% efficient.
The charge of each jet is unknown, making it very difficult
to distinguish between the particle and anti-particle from each W boson and
even the
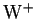 and
and
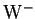 . The charge can be inferred by a jet charge technique [73]. This technique only has limited success for calculating the charge of
the di-jet pairs to identify the
. The charge can be inferred by a jet charge technique [73]. This technique only has limited success for calculating the charge of
the di-jet pairs to identify the
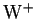 and
and
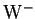 , but is almost useless when it
comes
to differentiating between the fractionally charged jets from the particle and
anti-particle.
, but is almost useless when it
comes
to differentiating between the fractionally charged jets from the particle and
anti-particle.
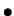
- The semi-leptonic decay is signified by two jets of particles
and a lepton.
Calculation of
the W production angle can be performed as all the momentum from the
hadronically decaying W boson can be measured. The problem of jet
pairing only arises if there is a
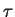 lepton
present and even in this case it is far reduced from the problem seen in the fully hadronic channel. ISR can still cause problems as once again
all the missing momentum is assigned to the neutrino.
Identification of the
lepton
present and even in this case it is far reduced from the problem seen in the fully hadronic channel. ISR can still cause problems as once again
all the missing momentum is assigned to the neutrino.
Identification of the
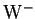 and
and
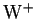 bosons is given by the lepton charge.
There is still an ambiguity in assigning the correct particles to each of the
two jets from the hadronically decaying W boson. Identification of which jet
represents the fermion and which the anti-fermion is also very difficult.
bosons is given by the lepton charge.
There is still an ambiguity in assigning the correct particles to each of the
two jets from the hadronically decaying W boson. Identification of which jet
represents the fermion and which the anti-fermion is also very difficult.
The semi-leptonic channel presents the fewest ambiguities when calculating the
five decay angles of the event, so is chosen as the signal process. The
polar and azimuthal
angle of either the decay fermion or anti-fermion in the W rest frame can be
calculated for each event. Thus the single W SDM elements can be calculated
from the
semi-leptonic decay events. For the W
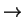 q
q
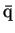 in the W-pair the
fermion and anti-fermion
cannot be distinguished, thus all the single W
SDM elements cannot be calculated from these.
in the W-pair the
fermion and anti-fermion
cannot be distinguished, thus all the single W
SDM elements cannot be calculated from these.
Certain projection operators (or combinations thereof) used to calculate
the SDM elements are invariant under the transform
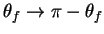 ,
,
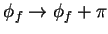 . This transform is
equivalent to the interchange of the fermion and anti-fermion from one of the
W bosons. Thus, these projection operators can be used on the hadronically
decaying W boson with the choice of fermion being arbitrary. The projection
operators that are invariant under this interchange include the following:
. This transform is
equivalent to the interchange of the fermion and anti-fermion from one of the
W bosons. Thus, these projection operators can be used on the hadronically
decaying W boson with the choice of fermion being arbitrary. The projection
operators that are invariant under this interchange include the following:
Therefore 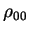 and
and 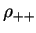 +
+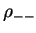 can still be extracted from the
hadronically decaying W boson. The combinations of SDM elements needed to
calculate the W-pair polarised cross-sections only require the combinations shown in equation 4.11, so may also be extracted from
the semi-leptonic events, as shown in equations 4.12-4.15. Both the individual W and W-pair polarised
cross-sections can then
be calculated from the semi-leptonic decay events.
can still be extracted from the
hadronically decaying W boson. The combinations of SDM elements needed to
calculate the W-pair polarised cross-sections only require the combinations shown in equation 4.11, so may also be extracted from
the semi-leptonic events, as shown in equations 4.12-4.15. Both the individual W and W-pair polarised
cross-sections can then
be calculated from the semi-leptonic decay events.




Next: Events with Final States
Up: Application to Data Events
Previous: Calculating the Polarised Cross-Sections
Contents
Jonathan Couchman
2002-11-04

![]() q
q
![]() in the W-pair the
fermion and anti-fermion
cannot be distinguished, thus all the single W
SDM elements cannot be calculated from these.
in the W-pair the
fermion and anti-fermion
cannot be distinguished, thus all the single W
SDM elements cannot be calculated from these.
![]() ,
,
![]() . This transform is
equivalent to the interchange of the fermion and anti-fermion from one of the
W bosons. Thus, these projection operators can be used on the hadronically
decaying W boson with the choice of fermion being arbitrary. The projection
operators that are invariant under this interchange include the following:
. This transform is
equivalent to the interchange of the fermion and anti-fermion from one of the
W bosons. Thus, these projection operators can be used on the hadronically
decaying W boson with the choice of fermion being arbitrary. The projection
operators that are invariant under this interchange include the following:
![]() and
and ![]() +
+![]() can still be extracted from the
hadronically decaying W boson. The combinations of SDM elements needed to
calculate the W-pair polarised cross-sections only require the combinations shown in equation 4.11, so may also be extracted from
the semi-leptonic events, as shown in equations 4.12-4.15. Both the individual W and W-pair polarised
cross-sections can then
be calculated from the semi-leptonic decay events.
can still be extracted from the
hadronically decaying W boson. The combinations of SDM elements needed to
calculate the W-pair polarised cross-sections only require the combinations shown in equation 4.11, so may also be extracted from
the semi-leptonic events, as shown in equations 4.12-4.15. Both the individual W and W-pair polarised
cross-sections can then
be calculated from the semi-leptonic decay events.