Event Reconstruction

So far, all the events that are likely to arise from W-pair production have been selected, however some of these may have very poorly measured elements and so the angular distribution of the particles cannot be well reconstructed. For the analysis of the W spins it is vital to have well reconstructed angles, so events without these need to be removed from the sample.

All events will have a track identified as the lepton. The electron direction is reconstructed by the tracking detectors and the energy is measured in the electromagnetic calorimeters. For the muons the momentum is measured using the tracking detectors. The case of the ${\rm W}^{+}{\rm W}^{-}\rightarrow{\rm q}\bar{\rm q}\tau\bar{\nu}_{\tau}$ event is slightly different, but this will either have one track or a narrow jet that is identified as the tau candidate. The energy of the $\tau$ candidate can only be derived from a kinematic fit.

Now, all the other tracks and calorimeter clusters can be said to have come from the hadronically decaying W boson. These are grouped into two jets using the Durham $k_{\bot}$ algorithm [68,69,70,71]. The total energy and momentum of each of the jets are calculated with the method described in [96].

To improve the quality of the measurement of the kinematical variables, a series of kinematically constrained fits are used:

For the ${\rm W}^{+}{\rm W}^{-}\rightarrow{\rm q}\bar{\rm q}{\rm e}\bar{\nu}_{\rm e}$ and ${\rm W}^{+}{\rm W}^{-}\rightarrow{\rm q}\bar{\rm q}\mu\bar{\nu}_{\mu}$ events kinematic fit A is performed. This fit uses five constraints, four from conservation of energy and momentum and one from the masslessness of the neutrino. This then gives one over-constraint and, hence is called the 1c fit. Events are accepted if this fit converges with a probability larger than 0.001. This requirement rejects about 2% of the signal events and 4% of the background.

To give further improvement in the angular observables a second kinematic fit can be applied to the events which passed the 1c fit. This fit, kinematic fit C, includes an additional contribution from the invariant mass of the charged lepton-neutrino system and another from the di-jet system. These two extra constraints, requiring the two W boson masses to be constrained by the average W boson mass measured at the Tevatron [97,98], then means that there are three over-constraints and this is then accordingly known as the 3c fit. The correct mass distribution is a Breit-Wigner with the central value at the Tevatron value. However, due to the difficulties of including the Breit-Wigner, the W mass distribution is treated as a Gaussian. In order to simulate the expected Briet-Wigner form, the variance of the Gaussian is updated at each iteration of the kinematic fit in such a way that the probabilities of observing the current fitted W mass are equal whether calculated using the Gaussian or the Briet-Wigner. Events are accepted if the 3c fit converges with a probability greater than 0.001. Around 4% of the events fail to do this, and for these the results from the 1c fit are reverted to.

For the ${\rm W}^{+}{\rm W}^{-}\rightarrow{\rm q}\bar{\rm q}\tau\bar{\nu}_{\tau}$ events kinematical fit B is applied. In addition to the 1c fit constraints, we have the extra constraint of the W bosons having equal mass. This results in one over constraint in the ${\rm W}^{+}{\rm W}^{-}\rightarrow{\rm q}\bar{\rm q}\tau\bar{\nu}_{\tau}$ events. This fit is required to converge with a probability greater than 0.025.

About 14% of the signal events are expected to fail this fit and so are rejected, however, about 41% of the selected background are also expected to fail this fit. The fit requirements also suppress those events which were correctly identified as ${\rm W}^{+}{\rm W}^{-}\rightarrow{\rm q}\bar{\rm q}\tau\bar{\nu}_{\tau}$ events, but where the $\tau$ decay products were identified incorrectly. The fraction of such events in the sample is reduced from 18% to 12%.

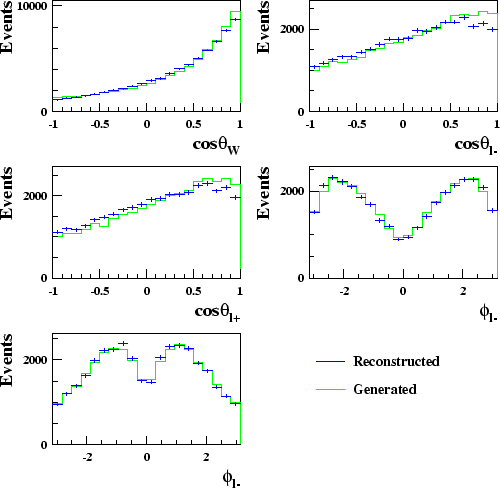
Figure 5.8 shows the distribution of kinematical variables of the selected events after the kinematical fits have been performed compared to the true distributions. Reasonable agreement is seen between the two.

**Figure 5.8:** The angular distributions for selected events only. The green histogram represents the true, generated angles. The blue points represent the reconstructed angles after the kinematic fits have been performed.
$\begin{figure}\begin{center} \epsfig{file=figs/reconang.eps,width=1.0\linewidth}\end{center}\end{figure}$