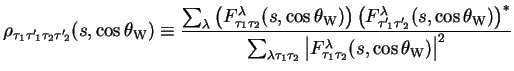The Two-Particle Joint Spin Density Matrix

The polarisation properties of the ${\rm W}^{\pm}$ bosons in the W-pair are completely described by the two-particle joint spin density matrix (SDM) [36,41], whose elements are given by:

$$\rho_{\tau_{1}{\tau^{\prime}}\!_{1}\tau_{2}{\tau^{\prime}}\!_{2}}... ...\left\vert F^{\lambda}_{\tau_{1}\tau_{2}}(s,\cos\theta_{\rm W})\right\vert^{2}}$$ (3.29)

The diagonal elements of the two-particle joint spin density matrix, which have $\tau_{1} = \tau_{1}^{\prime}$ and $\tau_{2} = \tau_{2}^{\prime}$ sum up to unity, i.e. the matrix has normalisation:

$$\sum_{\tau_{1}\tau_{2}}\rho_{\tau_{1}\tau_{1}\tau_{2}\tau_{2}}(s,\cos\theta_{\rm W}) = 1$$ (3.30)

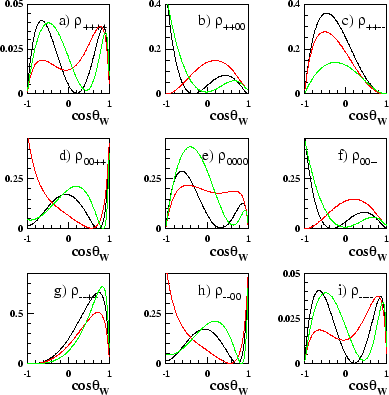
This normalisation occurs because the diagonal elements are effectively the probability of producing a pair of W bosons with helicity state $\tau_{1}\tau_{2}$. The off-diagonal elements are complex, but the diagonal elements are always purely real. The matrix elements are functions of both the centre-of-mass energy squared, $s$, and the W production angle, $\cos\theta_{\rm W}$. Examples of the analytical predictions for the diagonal elements as a function of $\cos\theta_{\rm W}$ can be seen in figure 3.10.

Figure 3.10: Examples of the diagonal elements of the two-particle joint W Spin Density Matrix. The black line is the Standard Model case and the red (green) line is for an anomalous coupling of $\Delta g^{z}_{1}$$=+$1 ($-$1).

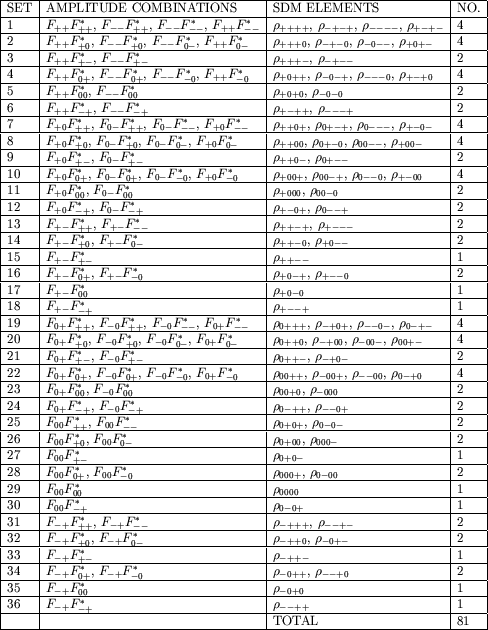
The two-particle joint density matrix is Hermitian and contains 81 elements. This means that, due to the normalisation given in equation 3.30, 80 of the elements are independent. However, if the W-pair production interaction is said to be CP-invariant, the helicity amplitudes fulfill the following relation:

$$F^{\lambda}_{\tau_{1}\tau_{2}}(s,\cos\theta_{\rm W}) = F^{\lambda}_{-\tau_{2}-\tau_{1}}(s,\cos\theta_{\rm W})$$ (3.31)

A consequence of enforcing CP-invariance upon the reaction is to reduce the number of independent elements in the density matrix from 80 to 35. This is demonstrated in table 3.5, where the combinations of helicity amplitudes, and thus the SDM elements, that are equivalent due to CP-invariance are grouped into 36 sets.

Table 3.5: The helicity amplitudes and thus the Spin Density Matrix elements that are related under CP-invariance. The helicity amplitude combinations in each set are equivalent to each other under CP-invariance. The SDM elements are those that correspond to each helicity amplitude combination. CP-invariance thus means that there are only 35 independent SDM elements.

As the two-particle joint density matrix contains all the information about the polarisation of the W bosons, the 5-fold differential cross-section given in equation 3.27 can now be written in terms of the joint density matrix, equation 3.32.

$$\frac{d\sigma({\rm e}^{+}{\rm e}^{-} \rightarrow {\rm W}^{+}{\rm ... ...W}d\cos\theta_{f_{1}}d\phi_{f_{1}}d\cos\theta_{\bar{f}_{4}}d\phi_{\bar{f}_{4}}}$$

$$= \frac{d\sigma({\rm e}^{+}{\rm e}^{-} \rightarrow {\rm W}^{+}{\rm W}^{-})}{d\cos\theta_{\rm W}}\left(\frac{3}{8\pi}\right)^{2}$$ (3.32)

$$\times \sum_{\lambda\tau_{1}{\tau^{\prime}}\!_{1}\tau_{2}{\tau^{\prime}}... ...\tau_{2}{\tau^{\prime}}\!_{2}}(\pi-\theta_{\bar{f}_{4}},\phi_{\bar{f}_{4}}+\pi)$$

The density matrix contains the probability of producing W-pairs of certain helicity states so the differential polarised cross-sections for producing final states of two transversely polarised W bosons (TT), two longitudinally polarised W bosons (LL), a transversely polarised ${\rm W}^{-}$ boson with a longitudinally polarised polarised ${\rm W}^{+}$ boson (TL) and a transversely polarised ${\rm W}^{-}$ boson with a longitudinally polarised polarised ${\rm W}^{+}$ boson (LT) can be written in terms of the elements in the joint density matrix [41], as shown in equation 3.33.

$$\frac{d\sigma_{\rm TT}}{d\cos\theta_{\rm W}} = \frac{d\sigma({\rm... ... e}^{-}\rightarrow{\rm W}^{-}_{\rm T}{\rm W}^{+}_{\rm T})}{d\cos\theta_{\rm W}} = \frac{d\sigma}{d\cos\theta_{\rm W}}\left(\rho_{++++}+\rho_{++--}+\rho_{--++}+\rho_{----}\right)$$

$$\frac{d\sigma_{\rm LL}}{d\cos\theta_{\rm W}} = \frac{d\sigma({\rm... ... e}^{-}\rightarrow{\rm W}^{-}_{\rm L}{\rm W}^{+}_{\rm L})}{d\cos\theta_{\rm W}} = \frac{d\sigma}{d\cos\theta_{\rm W}}\left(\rho_{0000}\right)$$ (3.33)

$$\frac{d\sigma_{\rm TL}}{d\cos\theta_{\rm W}} = \frac{d\sigma({\rm... ...{\rm e}^{-}\rightarrow{\rm W}^{-}_{T}{\rm W}^{+}_{\rm L})}{d\cos\theta_{\rm W}} = \frac{d\sigma}{d\cos\theta_{\rm W}}\left(\rho_{++00}+\rho_{--00}\right)$$

$$\frac{d\sigma_{\rm LT}}{d\cos\theta_{\rm W}} = \frac{d\sigma({\rm... ... e}^{-}\rightarrow{\rm W}^{-}_{\rm L}{\rm W}^{+}_{\rm T})}{d\cos\theta_{\rm W}} = \frac{d\sigma}{d\cos\theta_{\rm W}}\left(\rho_{00++}+\rho_{00--}\right)$$

From figure 3.10 it can be seen that $\rho_{++00}+\rho_{--00} = \rho_{00++}+\rho_{00--}$, even in the presence of anomalous couplings^3.4, so it intuitively follows that, as was stated earlier,

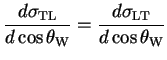$$\frac{d\sigma_{\rm TL}}{d\cos\theta_{\rm W}} = \frac{d\sigma_{\rm LT}}{d\cos\theta_{\rm W}}$$ (3.34)