
Job Traversal Times
Last Completion Times
Number of Transfers
A new virtual testbed was now devised in order to remove some of the quirks of the previous homogenous one, such as the anomalously effective performance of the round-robin scheduler. A hierarchy of resources like the MONARC Tier structure of Regional Centres was implemented, with one site given many machines and large data storage facilities, a few medium sized nodes, and several smaller ones. The total amount of processors, data and storage space was conserved, but distributed heterogenously, as shown in the table below. In addition Site 0, the largest node, was given a network connection of 0.1 GBytes / second, as opposed to the 0.01 GBytes / sec available to the other sites.
| Sites | No. Machines | Cache Size | No. Data Files | Max. Bitrate |
| Site 0 | 40 | 800 | 200 | 0.1 GBytes/sec |
| Sites 1-4 | 10 | 200 | 50 | 0.01 GBytes/sec |
| Sites 5-9 | 5 | 100 | 25 | 0.01 GBytes/sec |
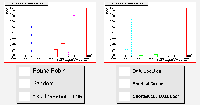
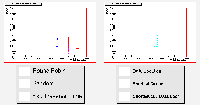
The six scheduling algorithms were again tested with a load of identically sized jobs, as described before, using this testbed. The results are shown in the plots below.

Job Traversal Times |

Last Completion Times |

Number of Transfers |
The uneven distribution of resources across the grid has finally caused the round-robin algorithm to falter, as the larger Site 0 is underloaded, and the smaller sites are given too many jobs to cope with. The random scheduler performs badly once more.
The algorithms sending jobs to the data also perform poorly in terms of job processing. The scheduler that makes decisions based purely on data location sends almost all of its jobs to the largest site, because there is a very high probability that it will host the greatest number of files in a list of ten chosen randomly from the available data. The algorithm that also takes queue length into account does only slightly better, because it only makes its "shortest queue" choice in the case of a tie between sites with an equal number of required data files. Both reduce the network traffic to an even greater extent than usual. This is because of the large number of files hosted at Site 0, meaning less data needs to be transferred there for jobs running on the local Compute Element.
The estimated traversal time scheduler is performing well here, as it is assigning identical jobs once more (the peaked structure has returned in the job traversal times, and is even appearing in the completion time plots). The minimum queue length algorithm is also doing well here. Both are loading the network less than the round-robin and random algorithms this time, because they are making effective use of the resources of Site 0.
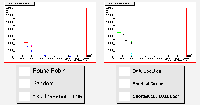
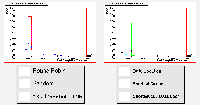
The final experiment was again performed with the heterogenous grid, but with jobs with the Gaussian distribution in CPU requirements as used earlier. The results are shown below:
Job Traversal Times |
Last Completion Times |
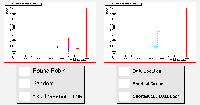
Number of Transfers |
There are few surprises here, as this set of results relates to those above in the same way that the corresponding experiments with a homogenous grid did. The peaked structure disappears again, and the performance of all six schedulers is degraded a little, with the more difficult task of scheduling jobs of varying size.
The estimated traversal time algorithm is struggling once more with these varying jobs. By some way, the most effective scheduler is the minimum queue length algorithm, as it does not make any inaccurate assumptions, and it responds well to feedback from the resources.
The results so far show that an intelligent strategy for scheduling can make a significant difference to the performance of a Grid, particularly if its topology is a heterogenous one with its resources unevenly distributed. A poor choice can lead to machines lying idle even when the workload elsewhere is greater than resources can handle.
Combining different strategies to improve scheduling decisions can produce good results, but a bad combination or even combining complementary strategies inappropriately can degrade performances significantly. For instance, the combination of algorithms looking for required data and minimum queue length produced very poor results with a heterogenous grid. However if it had applied these algorithms the other way around it would probably have given reasonable job processing times, while reducing network cost a little. There might be a more subtle way of combining these criteria to optimise the scheduling even further.
These preliminary results are intended to demonstrate that EDGSim is producing convincing results with the grid setup it is given. It is intended that some of the simplifications seen here will be removed, as the representation of the various EDG components is made more sophisticated. The experiments themselves will be improved, as more realistic grid topologies and job distributions are implemented.