The W-pair production process is characterised by a final state of four
fermions. It was shown in equation 3.27 that the cross-section
for the process
![]() may be written in terms of five angles,
the production angle of the
may be written in terms of five angles,
the production angle of the
![]() boson, the polar and azimuthal angles of
the
boson, the polar and azimuthal angles of
the
![]() decay fermion in the
decay fermion in the
![]() rest
frame,
rest
frame,
![]() ,
,
![]() and the polar and
azimuthal angles of
the
and the polar and
azimuthal angles of
the
![]() decay anti-fermion in the
decay anti-fermion in the
![]() rest frame,
rest frame,
![]() ,
,
![]() .
.
Monte Carlo generators can be used to generate pseudo-data events for the
process
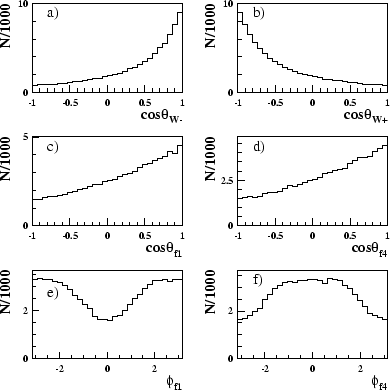
![]() . Figure 4.1 shows the Standard Model prediction
of the distributions of the five angles in W-pair
production and decay
calculated from events generated by the EXCALIBUR Monte Carlo generator.
. Figure 4.1 shows the Standard Model prediction
of the distributions of the five angles in W-pair
production and decay
calculated from events generated by the EXCALIBUR Monte Carlo generator.
 |
The equation
describing the 5-fold differential cross-section in terms of these angles
contains the
helicity amplitudes and the D-functions that described how the decay fermions
couple to the W bosons through the standard V![]() A coupling. This coupling, and
hence the angular distribution of the fermions depends on the helicity of
the W bosons.
A coupling. This coupling, and
hence the angular distribution of the fermions depends on the helicity of
the W bosons.
Measuring the angular distribution of the W decay products
then gives an effective way of measuring the W bosons' helicities.
The D-functions, given in equation 3.26, can be
inverted, so that rather than giving the angular distribution for a certain helicity, it will give the helicities for a certain angular distribution.
A set of
so-called projection operators [41] can thus be formed from
the D-functions.
When these operators are applied to the angular distributions of the decay
fermions, they effectively project out information about the helicities
of the W bosons. The projection operators are given the form of
![]() , where the
, where the ![]() and
and
![]() relate to the
interfering spins of individual W bosons, and the
relate to the
interfering spins of individual W bosons, and the ![]() indicates that there
is a different set of operators for the
indicates that there
is a different set of operators for the
![]() boson and
boson and
![]() boson. The full
set of projection operators can be seen in equation 4.1, where
boson. The full
set of projection operators can be seen in equation 4.1, where
![]() .
.
The single W SDM elements that describe the helicity properties of one of
the W bosons can
now be calculated using these projection operators. The
unnormalised single W density matrix elements can be extracted from the 3-fold
angular distribution of the
![]() decay fermion (or
decay fermion (or
![]() decay anti-fermion),
by
integrating with the appropriate projection operators, for example:
decay anti-fermion),
by
integrating with the appropriate projection operators, for example:
Each projection operator projects out information about one of the W bosons in
the W-pair. So, by integrating over combinations of the
![]() and
and
![]() projection operators, all 81 of the unnormalised two-particle joint SDMs can be
calculated, equation 4.3.
projection operators, all 81 of the unnormalised two-particle joint SDMs can be
calculated, equation 4.3.
If the full angular distributions of the decay fermion
from the
![]() and the decay anti-fermion from the
and the decay anti-fermion from the
![]() are known,
all the SDM elements can be calculated.
If the set of data are binned into bins of
are known,
all the SDM elements can be calculated.
If the set of data are binned into bins of
![]() , then experimentally
equation 4.2 can be realised as a discrete summation
over events, as in equation 4.4, where
, then experimentally
equation 4.2 can be realised as a discrete summation
over events, as in equation 4.4, where ![]() is the bin of
is the bin of
![]() ,
and
,
and ![]() is the number of events in that bin.
is the number of events in that bin.
The summations needed for each of the single
![]() SDM elements
are shown appendix A.1.
Performing these summations on the Monte Carlo data whose angular
distributions are shown in
figure 4.1 will give the single
SDM elements
are shown appendix A.1.
Performing these summations on the Monte Carlo data whose angular
distributions are shown in
figure 4.1 will give the single
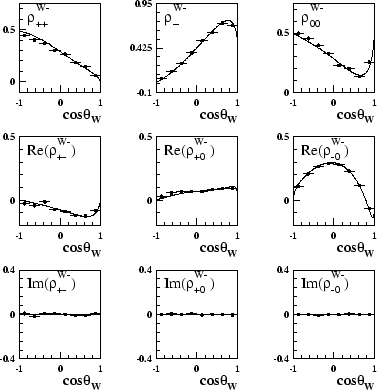
![]() SDM elements for this set
of data. These SDM elements are shown in figure 4.2. Overlaid are
the analytical predictions for the Standard Model calculated from equation 3.29.
SDM elements for this set
of data. These SDM elements are shown in figure 4.2. Overlaid are
the analytical predictions for the Standard Model calculated from equation 3.29.
 |
When calculating these SDM elements CPT-invariance can be assumed, so that
information from the
![]() and
and
![]() decay can be combined. CPT-invariance means
decay can be combined. CPT-invariance means
![]() .
Therefore, the summation to calculate each single W
.
Therefore, the summation to calculate each single W![]() SDM element may now be
written as a summation over the
SDM element may now be
written as a summation over the
![]() decays, plus a summation over the
decays, plus a summation over the
![]() decays
with the appropriate CPT transform applied to the projection operator.
decays
with the appropriate CPT transform applied to the projection operator.
The equation needed to calculate the single
![]() SDM elements
when both the
SDM elements
when both the
![]() decay fermion and the
decay fermion and the
![]() decay
anti-fermion are measured in every event is shown
in equation 4.5.
decay
anti-fermion are measured in every event is shown
in equation 4.5.
If only one of the W bosons is measured in each event, the
measurements from the
![]() and
and
![]() can still be combined to form just the single
can still be combined to form just the single
![]() SDM elements as shown in equation 4.6. In this equation
SDM elements as shown in equation 4.6. In this equation
![]() are the number of events with the
are the number of events with the
![]()
![]() decay
measured in
bin k of
decay
measured in
bin k of
![]() , and
, and
![]() are the number of events with the
are the number of events with the
![]()
![]() decay measured in bin k of
decay measured in bin k of
![]() . Thus
. Thus
![]() .
.
For the two-particle joint SDM elements both the decay fermion from
the
![]() and the anti-fermion of the
and the anti-fermion of the
![]() in the W-pair event need to be
measured.
Experimentally, equation 4.3 can also be written in
bins
of
in the W-pair event need to be
measured.
Experimentally, equation 4.3 can also be written in
bins
of
![]() as a discrete summation over events, as shown in equation 4.7.
as a discrete summation over events, as shown in equation 4.7.
The complete set of summations of operators giving all the two-particle joint
SDM elements
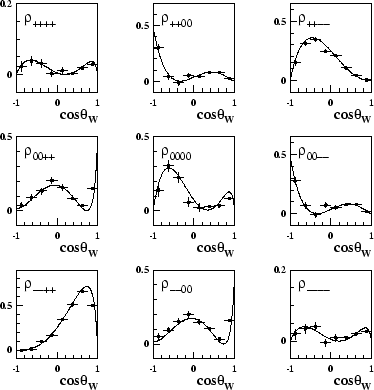
are given in appendix A.2. Taking, for example, the operators for
the diagonal elements
(
![]() ) of the
two-particle joint SDM and performing the summations on the Monte Carlo data,
the two-particle SDM elements shown in figure 4.3 are
obtained. Overlaid are
the analytical predictions for the Standard Model calculated from equation 3.29.
) of the
two-particle joint SDM and performing the summations on the Monte Carlo data,
the two-particle SDM elements shown in figure 4.3 are
obtained. Overlaid are
the analytical predictions for the Standard Model calculated from equation 3.29.
 |