Overcoming Problems of Detector Effects.

The SDM elements extracted from the data will not represent the true SDM elements. The less than perfect angular resolution, the finite selection efficiency and the acceptance of the OPAL detector are just some of the factors that will have an effect on the SDM elements. The data sample is expected to contain some background events and these will also cause deviation from the true SDM elements. The problem is increased further when you include such effects as ISR and the finite W width. Figure 6.1 indicates the extent of the problem detector effects cause. It shows the SDM elements extracted from a sample of fully detector simulated Monte Carlo events containing all possible signal and background processes. They have been passed through the same selection and reconstruction as is used for the data. Overlaid is the theoretical prediction for the Standard Model calculated from the purely analytical expression of the process ${\rm e}^{+}{\rm e}^{-} \rightarrow {\rm W}^{+}{\rm W}^{-} \rightarrow f_{1}\bar{f}_{2}f_{3}\bar{f}_{4}$, equation 3.29.

Figure 6.1: The Single W SDM elements extracted from a fully detector simulated Standard Model Monte Carlo sample. The solid line is the theoretical prediction calculated from the analytical expression.

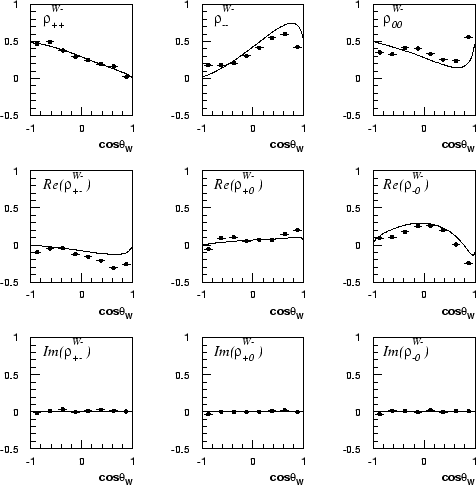The deviations due to the experimental effects are obvious in figure 6.1. The SDM elements extracted from the data cannot be directly compared with the theoretical predictions from the analytical formula, however they can be compared directly to SDM elements extracted from fully detector simulated Monte Carlo. The $\chi ^{2}$ curve is formed from the difference between SDM elements obtained from the data and from fully simulated Monte Carlo with different values of TGC.

A large number of samples of fully detector simulated Monte Carlo generated with a wide range of anomalous couplings are not available, so a different method is required to produce samples that can then be used in the $\chi ^{2}$ minimisation. A reweighting technique is employed to produce Monte Carlo samples with an arbitrary coupling. This method is discussed below.